Notes on neural mass models

PDF version: Notes on neural mass models – Logan Thrasher Collins      

Homogenous and heterogenous populations of neurons

• The simplest type of neural mass model involves assuming a homogenous population of neurons. This means that all neurons are coupled to each other and to themselves with an equal interaction strength w_ij=w₀. In graph theoretic terms, this is a complete graph with self-edges at every vertex. Furthermore, all neurons receive the same amount of externally applied current I^ext(t). As a consequence of these approximations, this type of model can only be used for large populations of neurons.
• Neural coupling strengths that are less than zero are inhibitory. Neural coupling strengths that are greater than zero are excitatory.
• Population activity is defined by the equation below. Note that this equation is not specific to homogenous populations, it can be used for many other types of models as well. N refers to the total number of neurons in the population while n_spikes counts the number of spikes between time t and a subsequent time t+Δt. The δ is the Dirac delta function and t_j^f is the time at which neuron j fires.

• The electrophysiological activities of integrate-and-fire neurons are defined by the following differential equation and its solutions where τ_m is the membrane time constant (which equals the membrane resistance R times the membrane capacitance C), I(t) is the input current, and u is the membrane voltage. If the value of u passes a threshold ϴ, then a spike occurs and u is reset to the resting potential u_rest.

• One of the tools necessary for describing the activity of a homogenous population of integrate-and-fire neurons is a function α(t – t_i^f) which represents the postsynaptic current generated by an input spike. Depending on the shape of the curve used to model the postsynaptic current, α(t – t_i^f) might take on different forms.
• With all neurons are coupled to each other (and to themselves) in a homogenous population, the total current in any given neuron is the externally applied current plus the sum of all postsynaptic currents from input spikes multiplied by each interaction weight w_ij.

• For homogenous populations with homogenous all-to-all coupling and a constant interaction strength w₀, the total current is the same in every neuron. This current is given by the following equation (since we can assume a continuum for a large population of neurons). The reason that the integral is multiplied by w₀N is that every neuron is connected to the given neuron. Here, s represents the time at which a spike occurs.

• Consider a population in which each neuron has slightly different parameters from the others such that the firing rates r_i(I(t)) vary over the population despite each neuron receiving the same input current. If the population is large, then the function which describes the variation in firing rate can be linearized around the average firing rate (and neglecting the higher-order terms of the Taylor series). As such, this simplification (the linearized model) can still be useful for some applications.

• The above expression can also be thought of as indicating that the mean firing rate of the population is equal to the firing rate of a “typical” neuron (with “typical” parameters) in the population.
• In cases that involve more dramatic variations within populations of neurons, the averaging technique described above is insufficient. For instance, consider a population in which half the neurons are described by a set of parameters p₁ and the other half by a set of significantly different parameters p₂. This population should be split and regarded as two homogenous populations.
• Indeed, any population composed of subsets which differ significantly from each other should be decomposed into the homogenous subsets. The same applies to populations composed of neurons with identical parameters, but with subsets that receive significantly different input currents.

Connectivity schemes and scaling

• Using these techniques, populations of different sizes can give similar results if a scaling law is applied to the connection weights. For a homogenous population with all-to-all connectivity, the appropriate scaling law is as follows. J₀ is the number of neurons before scaling and N is the number of neurons after scaling.

• Increasing the size of a population while keeping its connectivity the same allows for noise reduction. This is especially useful since some populations are quite small. For instance, a single layer within a cortical column might have only a few hundred neurons.
• Another all-to-all coupling model involves using a Gaussian distribution of weights with the following mean and standard deviation (σ₀ is the standard deviation of weights prior to scaling).

• Populations can also be modeled by setting a fixed coupling probability p (among N² possible connections). In this type of model, the mean number of connections to a neuron j is then given by pN and the variance is p(1 – p)N. Alternatively, each neuron j can send outputs to pN partners. To scale a population with a fixed coupling probability, the equation below is used so that the average number of inputs to each neuron does not change as the population size changes.

• Some simulations can assume a balanced population of excitatory and inhibitory neurons. In such cases, the mean input current is zero, so scaling the connection weights does not influence the mean. Instead, the weights should be scaled with respect to how they affect fluctuations about zero. This can be achieved using the following scaling equation.

Interacting populations

• In the previous sections, balanced populations of excitatory and inhibitory neurons were used. Now, consider homogenous populations each consisting of either excitatory or inhibitory neurons, but not both. 
• These populations can be visualized as spatially separated from each other, but this is not necessary for the model to work (and it is not biologically realistic). The populations could just as easily be spatially mixed.
• The activity of neurons in homogenous population n is given by the equation below. The parameter Γ_n represents the set of neurons belonging to population n.

• With all-to-all coupling, each neuron i within pool n is assumed to receive inputs from every neuron j within pool m. The connection strength is w_ij=J_nmN_m where J_nm is the strength of an individual coupling from a neuron in pool m to a neuron in pool n and N_m is the number of neurons in pool m. As such, the input current to a neuron i will come from all the spikes in the network. Once again, α represents some given type of postsynaptic voltage-time function after an input current.

• The input current can also be formulated by the equation below. Since the model provides identical input current to all neurons, the index i can be removed. Once again, s represents the time at which a spike occurs.

Distance-dependent connectivity

• To better model neural populations, distance can provide an approximate measure for coupling probability (with more distant neurons having a lower probability of coupling). It should be noted that this is still a very rough model. 
• In order to create a model with distance-dependent connectivity, each neuron i must be assigned a location x(i) on a two-dimensional cortical sheet.
• For this type of model, all connections are assigned the same weight and the connection probability depends on distance (see part A of the diagram). P is a function which maps any vector to a real number on the interval [0,1].

• Alternatively, all-to-all coupling can be assumed with a strength w_ij that decreases with distance (see part B of the diagram). This is modeled by the following equation where g is a function that maps any vector to a real number. (For example, a Euclidean length metric inside of a decaying exponential).

Spatial continuum models

• Many neural populations in the brain exhibit properties which continuously vary across space (i.e. tonotopy and retinotopy). Of course, this kind of variation is not actually continuous at the level of individual neurons, but it is effectively continuous from the perspective of population modeling. Sets of homogenous populations cannot account for such continuous variation, so spatial continuum models must be used when considering this kind of functional organization.
• Consider a continuum of neurons along a one-dimensional axis and assume all-to-all coupling with connection strength dependent upon distance. This model uses the equation w_ij = g(|x(i) – x(j)|) as described in the previous section. Then discretize space into segments of length d. The number of neurons in a segment n is given by the following equation where ρ represents the density of neurons. Neurons within this interval belong to the set Γ_m.

 

• For continuum models, the population activity of population m is described as a function of time and of the spatial position of the neurons belonging to population m. The latter is given by md since the distance along the axis is equal to the segment length times the index m.
• The coupling strength between a neuron x(i) at location nd and a neuron x(j) at location md is a function w(nd,md) that defines a weighting measure depending on the distance between the two locations nd and md.
• As such, the input current to a neuron in population m is computed using the following equation (top). The product of an input current from population n with the population activity induced in population m is found inside of the summation. All input currents to population m from the rest of the populations are then summed. For a large number of populations, this equation can be replaced by an equation with a second integral. For convenience, md has been replaced with y in these equations.

 

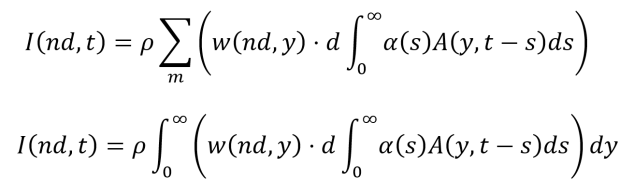
Reference: Gerstner, W., Kistler, W. M., Naud, R., & Paninski, L. (2014). Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition. New York, NY, USA: Cambridge University Press.