By Logan Thrasher Collins

Click here for PDF version

Click here for draft of a small-scale ExxRM proof-of-concept experimental protocol

Supplemental MATLAB code is located at the end of this page before the references

Combining synchrotron x-ray microscopy with expansion microscopy may represent a feasible approach for whole human brain connectomics at the nanoscale. Synchrotron x-ray microtomography on its own provides extremely fast imaging at high resolution, yet necessary tradeoffs between imaging throughput and resolution mean that the imaging an entire human brain with voxel sizes of less than 30 nm may still take much too long with current synchrotron technology. Fast imaging with voxel sizes of 300 nm is much more readily achievable. Furthermore, expansion microscopy isotropically enlarges tissue by infusion of a swellable hydrogel, facilitating resolution increases. The combination of x-ray microtomography and expansion microscopy (hereafter referred to as ExxRM) could thus push the effective voxel size down to the level needed for dense connectomics. However, because tissue volume and imaging time scale cubically with expansion factor, careful balance between design of the synchrotron x-ray optical setup and the degree of expansion will be needed. In particular, large high-resolution detectors will be vital. Additionally, methods to compensate for signal dilution from expansion and to stabilize expanded tissue under brilliant x-rays will be crucial. In this perspective, I will explore balances between synchrotron optical engineering choices and expansion factor, propose methods to successfully implement ExxRM in the context of human brains, and estimate how much it would cost to image the human brain in this way. Imaging brains via ExxRM may represent a crucial paradigm shift in connectomics which paves the way for holistic understanding of human brain function.

Introduction

Nanoscale connectomic imaging of the entire human brain represents a long sought-after goal that could provide the foundation for dramatic advances in neurobiology, neurotechnology, and artificial intelligence.^1,2 Currently, the leading method for nanoscale connectomics is volume electron microscopy (EM). But imaging a 1 mm³ volume of mouse cortex over a period of 6 months required a tremendous collaborative effort by Yin et al. to develop a parallelized and fully automated transmission electron microscopy (TEM) system consisting of six instruments working in parallel.³ Each of these six instruments cost $125,000. The mouse brain has a volume of roughly 500 mm³, meaning that if these numbers were directly scaled, the process would take 250 years.⁴ That said, Yin et al.’s TEM dataset had high resolution with 4×4×40 nm voxels, so throughput might be increased by imaging at somewhat lower resolution. As such, it is conceivable to argue that advances in EM technology may enable imaging of an entire mouse brain over the course of a few years. EM therefore represents a viable option for mouse brain connectomics. But the human brain’s volume is roughly 1200 cm³, around 2400-fold larger than the mouse brain.⁵ Even if EM technology somehow advances to the point where an entire mouse brain can be imaged in a single year for $10M, mapping a human brain with comparable parameters would take thousands of years. In my view, this provides a strong argument for the idea that a radically different approach is necessary for dense human brain connectomics and perhaps for dense connectomics in general.

Expansion light-sheet fluorescence microscopy (ExLSFM) represents a promising alternative to EM, yet this modality also falls short when considering the volume of the human brain (particularly after expansion). For instance, Lillvis et al. utilized 8-fold expansion and lattice light-sheet microscopy (ExLLSM) to image the Drosophila central complex in three colors with approximately 15×15×50 nm (including gain from expansion) voxels over the course of 5 days.⁶ But even accounting for the 8-fold expansion (512-fold volume increase), this amounts to a volume of less than 0.5 mm³. Imaging an 8-fold expanded mouse brain assuming these numbers would take 7009 years. Lattice light-sheet microscopes typically cost a few hundred thousand dollars each⁷ and might be parallelized enough to image an entire mouse brain within a year, particularly if further hardware optimization is achievable. Yet the 2400-fold larger volume of the human brain relative to the mouse brain indicates that ExLLSM human brain connectomics may still lay out of reach. Though some investigators have made strides in combining neuronal barcoding and ExLSFM and thus might be able to image at lower resolution, allowing human brain connectomics in a reasonable time frame through parallelization of thousands of light sheet microscopes instead of tens of thousands or more, there is still room for circumventing such expensive brute-force approaches. New methods are needed to facilitate faster dense human brain connectomics.

I suggest that a radically different strategy is needed to put the goal of human brain connectomics within reasonably close reach. Uniting synchrotron x-ray microtomography (XRM) (Figure 1A-B), expansion microscopy (ExM), and a recent staining method known as Unclearing Microscopy⁸ may facilitate ExxRM imaging of the human brain at sub-30 nm voxel size on timescales of around 1 year for a cost of around $10M. Success of this approach will necessitate overcoming some technical hurdles, yet I am optimistic that these particular challenges can be conquered. ExxRM may represent a feasible platform to acquire images suitable for dense connectomics across entire human brains.

Figure 1 Principles of synchrotron XRM. (A) Synchrotrons generate electrons from a source, propel them through a linear accelerator (linac), raise their energy in a booster ring, and then keep the electrons circulating for long periods of time at relativistic speeds in the storage ring. As relativistic electrons move along a curved path controlled by bending magnets, they emit brilliant x-ray beams in the direction tangent to the curve in the direction of the electron movement. Insertion devices that inject the x-rays into beamlines are placed at straight sections of the synchrotron ring. These insertion devices stimulate emission of bright and coherent beams into the experimental stations. (B) Microtomography beamlines receive an x-ray beam from an insertion device and filter out a narrow band of wavelengths using a monochromator. The beam passes through a sample on a rotating tomography stage that can be positionally adjusted to change the location of the field of view (FOV) within the sample. Projection images are taken across 360° of rotation. X-rays passing through the sample are converted to visible light using a scintillator, then directed by mirrors to a lens system that magnifies the image. This light hits a detector camera and data is recorded for 3D reconstruction.

Recommended methodologies for ExxRM

ExxRM’s success will require developing methodological strategies to mitigate technical challenges. Obtaining sufficient contrast to resolve subcellular features will be vital. ExM cubically dilutes the amount of cellular material per unit volume, so creative staining techniques will be needed. Approaches that ensure stability of expanded tissues under brilliant x-ray illumination for long durations will also be crucial. Multicolor imaging would greatly benefit the usefulness of whole brain connectomics data, so ways of efficiently obtaining tomograms in multiple colors are needed. These challenges must be conquered to translate ExxRM.

A central engineering hurdle for ExxRM is attaining sufficient feature contrast for capture of clear images. Because expanded tissues experience cubic dilution of target biomolecules, contrast from traditional stains such as osmium tetroxide almost entirely vanishes during x-ray microtomographic imaging (Collins et al., unpublished data). An elegant solution to this problem has come in the form of a recently developed technique called Unclearing Microscopy.⁸ For this technique, M’Saad et al. biotinylated primary amines (found on proteins, phosphatidylethanolamine lipids, etc.) throughout expanded samples, treated the sample with streptavidin horseradish peroxidase (streptavidin-HRP) fusion protein, and then stained with ionic silver reagents (from the EnzMet™ HRP Detection Kit) or with 3’3-diaminobenzidine (DAB). This triggered enzymatic deposition of enough chromogenic silver or DAB to make 20-fold expanded HeLa cells visible to the naked eye despite their 8000-fold increase in volume relative to the unexpanded state. Phase contrast light microscopy subsequently revealed subcellular features such as mitochondrial cristae, nuclear pore complexes, and nuclear membrane. Unclearing thus facilitates physical reconstruction of the structures that are pulled apart by ExM, filling in the gaps left by the expansion process (Figure 2A-B). Silver stain Unclearing could enable either absorption XRM or phase contrast XRM of expanded tissues since silver has excellent x-ray attenuation index β at relevant beam energies as well as excellent x-ray phase decrement δ. Focusing on phase contrast XRM may represent a better option since it can decrease the necessary dose of radiation per unit time by using x-ray wavelengths which are not absorbed as strongly by the tissue. Furthermore, phase contrast XRM is most sensitive to differences in sample density⁹ and silver staining forms dense precipitates of metallic silver (which in pure form has a high density of 10.49 g/cm³), so this approach might provide superior contrast in the context of ExxRM. Here, ExM’s sample dilution might prove advantageous because it could generate strongly distinct densities between silver-stained cellular features and the rest of the stabilized hydrogel. It should be noted that, for phase contrast XRM, the previously mentioned stabilization approach would need to fill the space between cellular features with a substance that differs substantially in density from the silver (or similar stain). Combining Unclearing Microscopy with phase contrast XRM could provide excellent feature contrast for ExxRM connectomics.

Expanded tissues are known for their fragility and synchrotron x-rays are known for their harshness, so strategies for solving the problem of sample degradation are needed. Newer expansion recipes which use high monomer concentrations have displayed substantially greater physical sturdiness than earlier generations of ExM hydrogels,^10,11 so this may aid in stabilization to some degree. Yet additional advances in ExM sample preparation may still be necessary due to high required fluxes and long imaging times. Cutting human brain samples into smaller volumes on the order of a few centimeters may improve the situation by decreasing imaging times per sample. Keeping the sample at cryogenic temperatures with the help of cryoprotectants to prevent ice crystals damaging the tissue may also help since heat generation from the x-rays is particularly problematic for hydrated samples.^12,13 That said, low temperatures would not fix the issue of radiation damage from ionization, so this issue should still be considered.¹⁴ Further stabilization might come in the form of infusion of a rapidly crosslinkable or crystalizing substance which irreversibly locks all biomolecules into place (Figure 2A-B). Polar uncharged fixatives such as glycol methacrylate may serve this purpose since they likely could substitute for water to facilitate expansion (Collins and Kohman, personal correspondence). Regardless of the specific reagents, it should be stated that the chosen substance would need to undergo an inducible crosslinking reaction that does not cause distortion of the expanded tissue. The chosen substance would need to undergo an inducible crosslinking or crystallization reaction that does not cause distortion of the expanded tissue, to not shrink or distort the expanded tissue while it diffuses into the hydrogel, and to minimally absorb x-rays at the energy range used for imaging, and to contrast sharply with the chosen stain material. So, the phase decrement of the stabilizing substance should be similar or lower compared to amorphous ice. This approach may enable sufficient stabilization to prevent nanoscale tissue degradation even with exposure to extremely brilliant synchrotron x-rays.

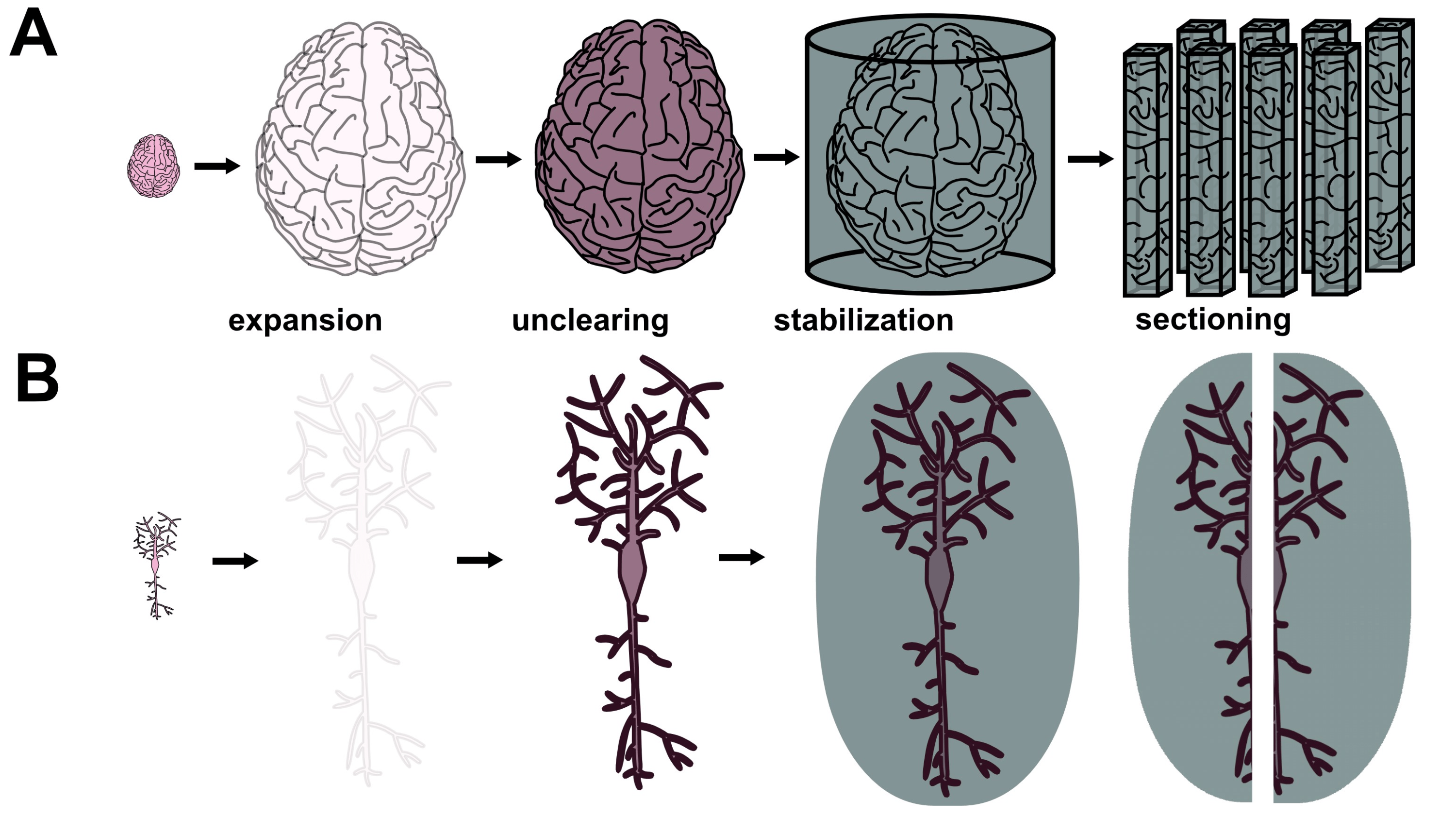
Figure 2 Proposed sample preparation technique for ExxRM. (A) Macroscale view of a human brain undergoing expansion, Unclearing, and stabilization. (B) Nanoscale view of a neuron within the brain undergoing expansion, Unclearing, and stabilization. Considerable amplification of signal density after Unclearing should occur.

Multicolor ExxRM would greatly enhance the value of acquired image data since synapses and key biomolecules could then be tagged within the 3D reconstruction.^15,16 Fortunately, multicolor absorption x-ray microscopy represents an established technique wherein two or more staining materials undergo two or more rounds of imaging at beam energies corresponding to the absorption edges of the chosen materials. The absorption edges in question must be sufficiently distinct that minimal overlap in detection occurs across the different beam energy imaging rounds. As an example, Depannemaecker et al. employed this approach by using antibody-linked gold nanoparticles to mark neuronal nuclei in mouse brains while also staining neurons with silver via Golgi’s method.¹⁵ They imaged at a beam energy corresponding to an absorption edge of silver and at a beam energy corresponding to an absorption of gold. In addition, multicolor phase contrast x-ray imaging might be accomplished by using molecularly targeted tags with distinct densities relative to the Unclearing silver stain. For instance, gold has a density about twice that of silver, so it might be possible to segment gold nanoparticles after data acquisition. A potential challenge for these methods comes from the difficulty of inducing reliable diffusion of large metallic nanoparticles into tissue. That said, post-expansion pre-stabilization staining could help overcome the problem since expanded gels are typically more porous than pre-expansion tissue. Multicolor ExxRM in 2-3 colors should be achievable, opening doors to more useful whole-brain image datasets.

Though some trial and error will doubtless prove necessary for ExxRM optimization, the required technologies lay within fairly close reach. High contrast could be achieved by applying Unclearing Microscopy to counter signal dilution from expansion. Stability under brilliant x-rays may be possible by leveraging stabler expansion recipes with higher monomer concentrations, by cutting the brain into centimeter-scale subvolumes to decrease radiation dose per sample, by employing cryogenic temperatures during imaging, and by developing rigidity-enhancing materials to infuse into expanded gels. Multicolor ExxRM could be achieved by staining with metallic nanoparticles linked to affinity reagents and performing additional scans tuned to the absorption edges of the chosen metals. These directions may provide a path towards successful ExxRM.

How fast can synchrotrons image expanded brains?

Synchrotron facilities offer bright and coherent x-rays that can rapidly image large volumes of tissue at high resolutions (Figure 1A-B). In this regard, a recent international connectomics consortium known as SYNAPSE (Synchrotrons for Neuroscience: an Asia-Pacific Scientific Enterprise) has highlighted the value of synchrotron XRM for imaging large animal brains.¹⁷ Unfortunately, SYNAPSE does not employ ExM and is thus limited to 300 nm resolution, making their connectomics approach unsuitable for dense reconstruction of neuronal connections. At this resolution, they can only roughly reconstruct neuronal projections and certainly cannot identify synapses. Nonetheless, SYNAPSE has made technical strides towards optimizing the engineering of synchrotron beamlines towards whole-brain imaging applications. In particular, they report acquiring x-ray projection images in as little as 1 millisecond by utilizing a high-photon-energy cut-off mirror and certain filters in place of a monochromator (and “white” radiation is employed).^17,18 Based on the Crowther limit,¹² the number of projections N_θ needed to completely reconstruct a single tomogram is described by the equation N_θ = (π/2)N where N is the number of pixels along the horizontal direction of the image. So, for an image with N = 1000, the tomogram will require up to 3142 projection images. If each projection takes 1 ms to acquire, this means that one could potentially obtain such a tomogram in just over 3 seconds. Importantly, one should realize that larger tomograms will overall increase imaging speed despite necessitating more projections since the tomogram size scales volumetrically and the projection number only scales linearly. So, the largest possible detectors should be utilized given engineering constraints (described in next paragraph). With these metrics, one can calculate whether synchrotron microtomography might image entire expanded brains and help determine what expansion factor to use for reaching sub-30 nm voxel size while still imaging over reasonable timeframes.

Given the information described above, one may estimate optimal parameters for ExxRM (Table 1, Supplemental Code File 1). To achieve sub-30 nm pixel size, a recently developed form of ExM known as “Magnify”, which features lipid and protein retention, high physical stability, and 11-fold expansion of brain tissue may represent an ideal technique.¹⁰ At 11-fold expansion and 300 nm pixel size, effective voxel size would reach 27 nm, sufficient for dense connectomics. To image rapidly enough to acquire the entire human brain in one year, tradeoffs between detector size and pixel size must be considered. Synchrotron XRM typically uses a scintillator to convert x-rays into visible light prior to magnification via a visible light objective lens, which means the field of view (FOV) is limited by this objective lens and by how many sufficiently small pixels can be packed onto a detector. Generally, the lower the magnification of the objective lens, the wider its FOV. Yakovlev et al. demonstrated a technical accomplishment showing the feasibility of combining large FOV with high resolution.¹⁹ They developed a custom objective lens with a magnification of 6.2× and coupled it to a detector with 3.1 µm pixel size and FOV of 5 mm by 3.5 mm (10000 pixels by 7096 pixels). This enabled reconstruction of tomograms with diameter of 5 mm, height of 3.5 mm, and isotropic voxel size of 500 nm. Similar engineering of detectors and objectives might be used for mouse brain connectomics. But for human brain connectomics, one would likely need to focus on constructing a massive detector while maintaining 300 nm pixels to circumvent the probably much greater challenge of developing an objective lens with a FOV in excess of 75 mm. Imaging the entire human brain in less than one year at 27 nm effective voxel size would necessitate either a detector consisting of 62000×62000 300 nm pixels (18.6 mm × 18.6 mm and a tomogram volume of volume of about 5054 mm³)or an even vaster detector with larger pixels coupled to an objective lens with a perhaps unrealistically massive FOV. Projections acquired with such a device would require 97389 projections per tomogram according to Crowther’s limit.¹² While this envisioned technology still falls beyond what has previously been achieved even in the case of Yakovlev et al., it is conceivable that current or near-future technology might allow such an objective-detector system to be commissioned for just a few million dollars, particularly given that emerging commercial smartphone cameras can now employ 200 million pixels of 560 nm and similar systems with smaller pixels are under development.²⁰ Effective detector size might also be improved if a smaller detector panel is tiled across a larger light beam (e.g. take four images per projection of a single detector at four different tiled positions). This would linearly increase imaging time but could lead to sizable increases in overall volume acquisition speed. That said, the impact of transition time would need to be considered and might represent a significant issue. It should be noted that camera bandwidth for data recording and transmission, minimizing transition time for moving the sample between tomograms, and the time cost of slightly overlapping tomogram volumes will also need to be considered. Combining a large enough detector system with sufficiently powerful x-ray beam flux per mm² to achieve 1 millisecond projection acquisition times (as described by the SYNAPSE consortium¹⁷), may make a human brain connectome image dataset with 27 nm effective voxel size obtainable in approximately one year of continuous imaging.

Table 1 Comparison of parameters necessary for ExxRM acquisition of a human brain connectome image dataset in 1 year at 27.27 nm effective voxel size with a mouse brain connectome image dataset in 1 month at 27.27 nm effective voxel size.

As an additionally useful metric for evaluation, Du et al. offer a mathematical model to estimate the number of photons needed for imaging a sample with sufficient contrast to distinguish between voxels of desired size.¹² The model starts by considering how many photons n̄_pixel are needed to image a single pixel on a tomographic slice. The pixel is assumed to contain a “feature” material with a phase decrement δ_f that must be distinguished against a background with a phase decrement δ_b. Distinctions can be made between adjacent background pixels b, overlaying background pixels b_o’ and underlaying background pixels b_u’. The SNR is assumed to equal 5 as based on the Rose criterion, which qualitatively represents an acceptable SNR for visually useful images. Background attenuation coefficient is given by µ_b’ and the thicknesses of the overlaying and underlaying background material are t_b’o and t_b’u respectively. After the value of n̄_pixel is determined, the value is multiplied by the square N² of the number of pixels N on the detector’s horizontal axis to find the number of photons needed per tomogram. As Du et al. explain, the number of slices is not used as a multiplicative factor since the photons are distributed across all of the rotation angles for each pixel. These calculations act as a guide to what sample properties and beam properties are needed for ExxRM.

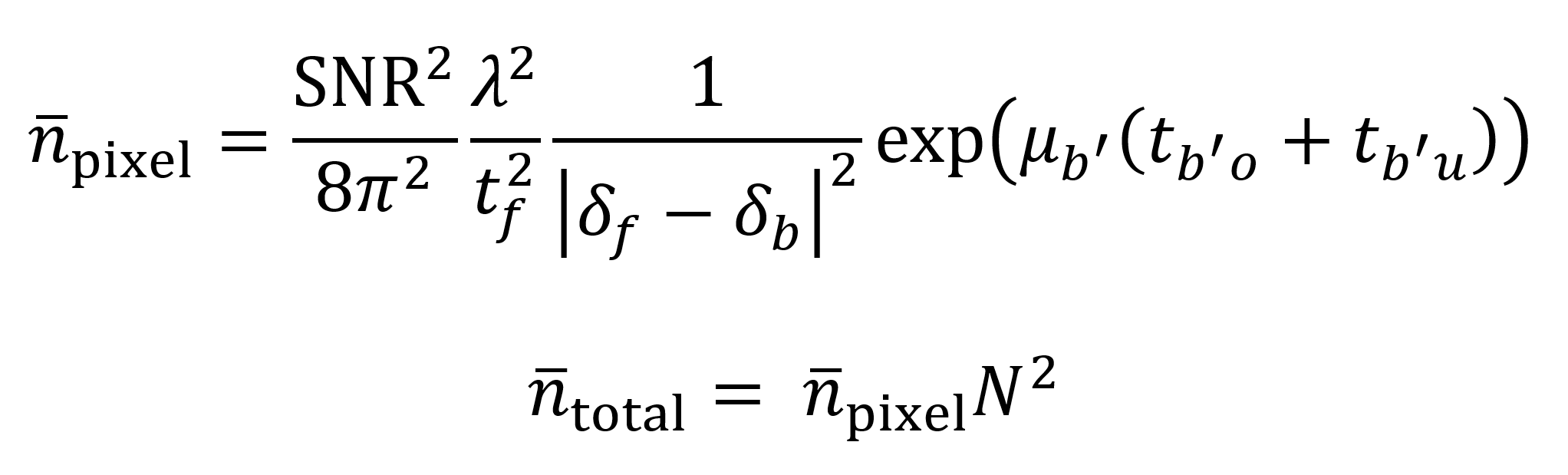
The Du et al. model can help determine the feasibility of ExxRM by estimating the necessary flux to image the expanded brain at a desired voxel size in a reasonable time frame. Consider as an example a cube-shaped 0.3 cm³ piece of brain tissue expanded 11-fold to a block with dimensions of 3.3×3.3×3.3 cm. Based on this, assume that the average thickness of overlaying and underlaying background material is 1.65 cm (though the actual value will of course vary with the depth into the sample). Also assume that the background material is made of amorphous water ice with a density of 0.92 g/cm³. By using the Unclearing Microscopy technique, expanded features might be “filled in” after a metallic silver stain.⁸ Thus, I will assume that the 11-fold expanded features are made up of metallic silver with a density of 5.25 g/cm³, half the density of pure metallic silver (to account for imperfect staining). Feature phase decrements δ_f, background phase decrements δ_b, and background attenuation coefficients µ_b’ across x-ray energies ranging from 10 keV to 30 keV can be obtained using the calculator available at (https://henke.lbl.gov/optical_constants/pert_form.html) which is based on the Henke dataset.²¹ This calculator does not directly give µ_b’, but it does give attenuation index β, for which µ_b’ = 4πβ/λ. According to the resulting model (Supplemental Code File 2), the total number of photons needed to image a single tomogram (volume of 5054 mm³) using the described 18.6 mm × 18.6 mm detector within the given 11-fold expanded block at an energy of 30 keV is about 1×10¹⁴, which is within the capabilities of some contemporary synchrotrons, particularly since the flux per mm² comes out to roughly 2.89×10¹¹ photons/mm² after dividing by the area of the detector.

Du et al. also give an equation (see below) for estimating the radiation dose D_f imparted to a given feature in units of Gray (Gy) where 1 Gy equals 1 J of energy per kilogram of material. Leveraging the model described above (Supplemental Code File 2), this would give 0.0032 Gy as the dose imparted to a feature or 3.46×10¹¹ Gy per 5054 mm³ tomogram. Though past studies have successfully imaged small specimens subject to comparable doses of radiation,²² this still represents a higher level of exposure than is desirable. As such, the stabilization measures (beyond just keeping the sample at cryogenic temperature during imaging) described earlier might be necessary to maintain sample integrity. Gathering experimental data on tolerable radiation dose for this specific situation will represent a vital step to clarify what engineering approaches are needed to circumvent radiation issues.

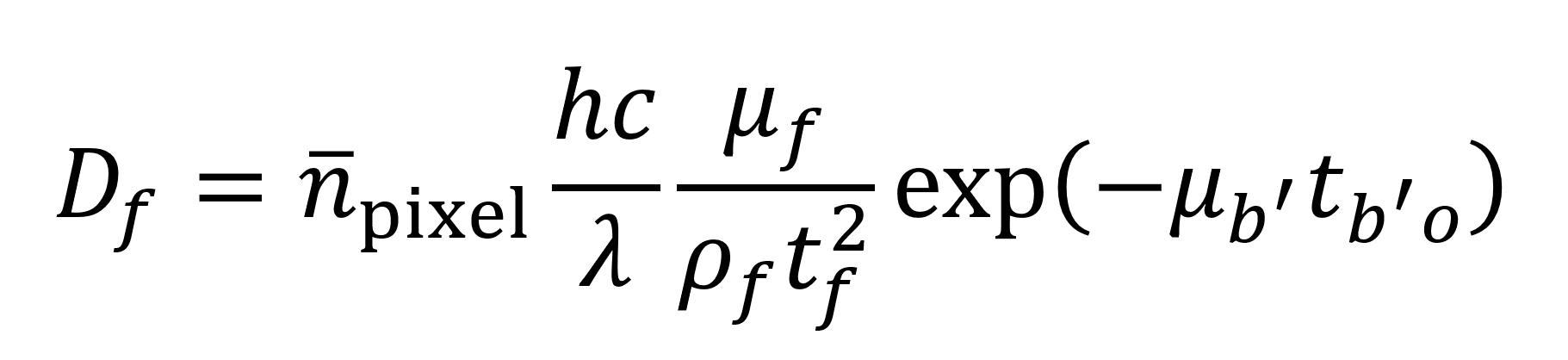
Cost estimates for whole brain ExxRM

While the power of the synchrotron facility comes with a high price tag, ExxRM may still represent the most overall cost-effective option for human brain connectomics. Consider the costs associated with the DLS as an illustrative example. The DLS is a third-generation facility and is currently one of the better synchrotrons in terms of its ability to produce bright and coherent x-rays. Building the DLS and its first seven beamlines from 2003-2007 cost about $316M, its later upgrades cost $144M and $134M, and its yearly operational costs have increased from $28M in 2007-2008 to $81M in 2019-2020 (Table 2). Based on these data points, construction of a new synchrotron beamline costs approximately $10M and yearly maintenance may cost roughly $500K. This provides a framework for estimating the cost of a dedicated human brain ExxRM connectomics beamline.

Table 2 Costs associated with the Diamond Light Source²³ as a case study on how much money is needed to build and maintain a state-of-the-art synchrotron facility.

Compact Light Source (CLS) technology should be considered as well before continuing. CLS instruments produce x-ray beams that fall somewhere between laboratory x-ray microscopes and synchrotrons in terms of brightness and coherence.²⁴ CLS instruments are furthermore small enough to fit into a single room and are inexpensive enough that a large number of them could potentially be constructed in parallel. At first glance, CLS technology seems a more economically viable alternative to synchrotron beamlines, yet it still probably is not a good option at this time. Existing CLS instruments are not likely suitable for human brain (or even mouse brain) ExxRM connectomics in the foreseeable future because their optical engineering requirements and mediocre level of x-ray flux preclude rapid tomography at submicron resolution, particularly when a large field of view is desired.²⁵ There is a small possibility that future advances in CLS technology could change this situation, yet this seems fairly unlikely, so synchrotron-based imaging remains the best route.

Building an entire synchrotron solely for ExxRM connectomics is probably less efficient than establishing an agreement with an existing synchrotron to construct a connectomics beamline. While one might envision additional parallelization through custom design of the beamline to split the beam to land in multiple sample chambers, splitting the beam would divide the photon flux and therefore increase imaging times for no net gain in speed. As such, parallelization would likely require an additional insertion device and thus an entire new beamline for each new sample chamber. Insertion devices consist of a series of precisely engineered magnets built into straight sections of the synchrotron’s ring. These magnets, known as undulators or wigglers depending on the specifics of the insertion device, stimulate directed emission of a brilliant x-ray beam out from the storage ring.²⁶ Yet even if we assume $10M total plus yearly maintenance costs for each connectomics beamline, imaging multiple human brains over the course of a year or a single human brain in just a few months remains a reasonable proposition. For a project as important as mapping the human brain at sufficient resolution for dense neuronal reconstruction, price tags in the range of tens of millions of dollars may not be out of reach.

Conclusion and outlook

Connectomics needs a technological paradigm shift if it is to feasibilize dense mapping of one or more human brains. Though it comes with some technical challenges, ExxRM may represent a key strategic shift that drastically reduces human brain connectomics timelines from centuries down to 1-2 years for the image acquisition step. Data storage and early processing steps will of course require data centers and high-performance computing, but this field is rapidly advancing and may indeed be capable of handling the challenge. New algorithmic advances and machine learning technologies may help tomographic reconstruction keep pace with imaging data acquisition. Assuming 1 byte per voxel, the amount of storage needed for an 11-fold expanded human brain with 300 nm physical voxel size (27 nm effective voxel size) is about 61 exabytes. Segmentation of the human brain dataset will probably represent a vastly more difficult problem as well as require substantially more compute resources, so further advances in this area will need to occur in parallel with ExxRM development. Realizing the benefits of connectomics in the form of complete computational models of the brain will take additional extensive research. Precisely correlating gene expression and electrophysiological properties with neuronal morphology (i.e. “cell type”) may represent a major step towards bridging the divide between structural data and functional activity. Nonetheless, the allure of having a holistic anatomical picture of the brain may serve as a driving force in the meantime, especially given the clinical implications of this connectome. ExxRM has the potential to transform the dense connectomics field, enabling anatomical imaging of the entire human brain with sub-30 nm voxel size in around a year for a price of roughly $10M.

Supplemental code

Copy and paste each code into a MATLAB script and run, modify as needed:

Supplemental Code 1

% optimization of ExxRM tomographic metrics calculations

% vary detectorpixels_on_a_side
detectorpixels_on_a_side = 62000; %[62000 human; 4334 mouse]; % assume that large detectors and big beams are possible
dponas = detectorpixels_on_a_side; % square detector pixels on a side, see above
pixelsize = 300; % nm; assume this size can be achieved
squaredetectorsize_on_a_side_mm = dponas.*(pixelsize*10^-6);
npixels_slice = dponas.^2; % total number of pixels on n x n detector
projections = dponas*(pi/2); % based on Du et al. equation 7, Crowther's limit

% vary pixelsize, expansionfactor
singleprojectiontime = 0.001; % seconds; very fast, as seen in https://doi.org/10.1016/j.physrep.2022.11.003 and https://doi.org/10.1107/S1600577521007633
expansionfactor = 11; % vary with [4; 4.5; 8; 10; 11; 16; 20; 25]

% effectivepixelsize should be 30 nm or less
effectivepixelsize = pixelsize/expansionfactor % effective pixel size post-expansion

tomogramvolume_voxels = dponas.*pi.*(dponas./2).^2; % cylindrical tomogram volume in number of voxels
tomogramvolume_mm3 = tomogramvolume_voxels*(pixelsize^3)/(10^18); % cylindrical tomogram volume in mm3
tomogramtimeseconds = singleprojectiontime*projections % time per tomogram

humanbrainvolume = 1200*1000; % mm^3
mousebrainvolume = 500; % mm^3

% human brain calculations 
expandedhumanbrainvolume = humanbrainvolume*(expansionfactor^3); % mm^3
totaltomograms_humanbrain = expandedhumanbrainvolume./tomogramvolume_mm3; % number of tomograms needed for whole expanded human brain
totalimagingtimeseconds_humanbrain = totaltomograms_humanbrain.*tomogramtimeseconds; % seconds
secondsperyear = 3.154*10^7; % number of seconds in a year
totalimagingtimeyears_humanbrain = totalimagingtimeseconds_humanbrain/secondsperyear; % years
format longG;
totalimagingtimeyearshumanbrain_squaredetectorsizeonsidemm = [totalimagingtimeyears_humanbrain, squaredetectorsize_on_a_side_mm]

% mouse brain calculations 
expandedmousebrainvolume = mousebrainvolume*(expansionfactor^3); % mm^3
totaltomograms_mousebrain = expandedmousebrainvolume./tomogramvolume_mm3; % number of tomograms needed for whole expanded human brain
totalimagingtimeseconds_mousebrain = totaltomograms_mousebrain.*tomogramtimeseconds; % seconds
totalimagingtimeyears_mousebrain = totalimagingtimeseconds_mousebrain/secondsperyear; % years
format longG;
totalimagingtimeyearsmousebrain_squaredetectorsizeonsidemm = [totalimagingtimeyears_mousebrain, squaredetectorsize_on_a_side_mm]

Supplemental Code 2

% calculations of photon flux for ExxRM

%expansion x-ray microscopy radiation dose calculations based on Du et al. at 30 keV energy for silver at 5.25 g cm^-3
rhof_percm3 = 5.25; % g/cm^3 or use 10.49 g/cm^3 for 'silver_constants.mat'
rhof = rhof_percm3./(10^21); % density in g/nm^3
venergy = 2.9672*10^4; % source is calculator (Ag 5.25 g cm^-3) at https://henke.lbl.gov/optical_constants/getdb2.html
vdelta = 1.0086*10^-6; % source is calculator (Ag 5.25 g cm^-3) at https://henke.lbl.gov/optical_constants/getdb2.html
vbeta = 6.1419*10^-8; % source is calculator (Ag 5.25 g cm^-3) https://henke.lbl.gov/optical_constants/getdb2.html
venergybackground = 2.9672*10^4; % source is calculator (H2O 0.92 g cm^-3) at https://henke.lbl.gov/optical_constants/getdb2.html
vdeltabackground = 2.4086*10^-7; % source is calculator (H2O 0.92 g cm^-3) at https://henke.lbl.gov/optical_constants/getdb2.html
vbetabackground = 1.0051*10^-10; % source is calculator (H2O 0.92 g cm^-3) at https://henke.lbl.gov/optical_constants/getdb2.html
snr = 5; % desired signal-to-noise ratio, value of 5 is Rose criterion
E = venergy; % energy range in eV
hc = 1239; % Plank's constant times the speed of light in units of eV nm
lamda = hc*(E.^-1); % x-ray wavelength at energy E
tf = 300; % feature thickness with expansion (nanometers)
deltaf = vdelta; % phase shift of feature composed of silver
deltab = vdeltabackground; % phase shift of background composed of amorphous ice with density 0.92 g cm^-3
betaf = vbeta; % absorption index of feature composed of silver
betab = vbetabackground; % absorption index of background composed of amorphous ice with density 0.92 g cm^-3
mupb = 4*pi.*betab./lamda; % mu'b, attenuation coefficient (nm^-1) of background over and under feature (not adjacent)
mub = 4*pi.*betab./lamda; % mub, attenuation coefficient (nm^-1) of background adjacent to feature
muf = 4*pi.*betaf./lamda; % mub, attenuation coefficient (nm^-1) of feature
tbo = 16500000; % average thickness of background over feature (nm), assuming 0.3 cm^3 block 11x expanded to 3.3 cm side length
tbu = 16500000; % average thickness of background under feature (nm), assuming 0.3 cm^3 block 11x expanded to 3.3 cm side length

% primary useful x-ray properties calculator https://henke.lbl.gov/optical_constants/getdb2.html
% another useful x-ray properties calculator http://purple.iptm.ru/xcalc/xcalc_mysql/ref_index.php

npixel_phase = ((snr^2)/(8*pi^2)).*((lamda.^2)./(tf.^2)).*(((abs(deltaf-deltab)).^-2)).*exp(mupb.*(tbo+tbu));
% photons per pixel needed for phase contrast imaging of a feature f

npixel_absorption = ((snr^2)/(8*pi^2)).*((lamda.^2)./(tf.^2)).*(((abs(betaf-betab)).^-2)).*exp(mupb.*(tbo+tbu));
% photons per pixel needed for absorption imaging of a feature f

square_detector_side_pixels_mm = 62000; % assume 300 nm pixel size on a 18.6 mm by 18.6 mm detector
npixels_tomo = npixel_phase*square_detector_side_pixels_mm^2; % Du et al. equation 8 gives total photons per tomogram
slices = square_detector_side_pixels_mm*(pi/2); % estimated number of slices required for tomographic reconstruction, given by N pixels on side length times pi/2

% Note: not every pixel contains a feature, but for now, we will assume that this is not the case
featuredensity = 1;
photons_tomo = featuredensity*npixels_tomo % total photons needed to image a tomogram in this situation

radiation_dose_npixelDf = npixel_phase.*(hc./lamda).*(muf./(rhof.*(tf.^2))).*exp(-mupb*tbo); % units of eV/g
C = (1.60218*10^-19)/1000% Multiplicative factor C to convert eV/g to J/kg
Df = C*radiation_dose_npixelDf % radiation dose in Gray (Gy) imparted to each feature. Multiplicative factor C converts eV/g to J/kg
Dftomo = photons_tomo.*Df

References

1.        Collins, L. T. The case for emulating insect brains using anatomical “wiring diagrams” equipped with biophysical models of neuronal activity. Biol. Cybern. 113, 465–474 (2019).

2.        Koene, R. A. Fundamentals of whole brain emulation: state, transition, and update representations. Int. J. Mach. Conscious. 04, 5–21 (2012).

3.        Yin, W. et al. A petascale automated imaging pipeline for mapping neuronal circuits with high-throughput transmission electron microscopy. Nat. Commun. 11, 4949 (2020).

4.        Badea, A., Ali-Sharief, A. A. & Johnson, G. A. Morphometric analysis of the C57BL/6J mouse brain. Neuroimage 37, 683–693 (2007).

5.        Cosgrove, K. P., Mazure, C. M. & Staley, J. K. Evolving Knowledge of Sex Differences in Brain Structure, Function, and Chemistry. Biol. Psychiatry 62, 847–855 (2007).

6.        Lillvis, J. L. et al. Rapid reconstruction of neural circuits using tissue expansion and light sheet microscopy. Elife 11, e81248 (2022).

7.        Watkins, S. C. & St. Croix, C. M. Light sheet imaging comes of age. J. Cell Biol. 217, 1567–1569 (2018).

8.        M’Saad, O., Shribak, M. & Bewersdorf, J. Unclearing Microscopy. bioRxiv 2022.11.29.518361 (2022) doi:10.1101/2022.11.29.518361.

9.        R A Lewis. Medical phase contrast x-ray imaging: current status and future prospects. Phys. Med. Biol. 49, 3573 (2004).

10.      Klimas, A. et al. Magnify is a universal molecular anchoring strategy for expansion microscopy. Nat. Biotechnol. (2023) doi:10.1038/s41587-022-01546-1.

11.      M’Saad, O. & Bewersdorf, J. Light microscopy of proteins in their ultrastructural context. Nat. Commun. 11, 3850 (2020).

12.      Du, M. et al. Upscaling X-ray nanoimaging to macroscopic specimens. J. Appl. Crystallogr. 54, 386–401 (2021).

13.      Matsuyama, S. et al. Elemental mapping of frozen-hydrated cells with cryo-scanning X-ray fluorescence microscopy. X-Ray Spectrom. 39, 260–266 (2010).

14.      Lombi, E. et al. Fast X-Ray Fluorescence Microtomography of Hydrated Biological Samples. PLoS One 6, e20626 (2011).

15.      Depannemaecker, D. et al. Gold Nanoparticles for X-ray Microtomography of Neurons. ACS Chem. Neurosci. 10, 3404–3408 (2019).

16.      Logan Thrasher Collins, Kayla Siletti, Kristine Fischenich, Jennifer Coulombe, Nathan Anderson, M. S. Structural brain mapping using antibody-conjugated gold nanoparticles and x-ray microscopy. in Society for Neuroscience Conference (2019).

17.      Stampfl, A. P. J. et al. SYNAPSE: An international roadmap to large brain imaging. Phys. Rep. 999, 1–60 (2023).

18.      Chen, H. H. et al. High-resolution fast-tomography brain-imaging beamline at the Taiwan Photon Source. J. Synchrotron Radiat. 28, 1662–1668 (2021).

19.      Yakovlev, M. A. et al. A wide-field micro-computed tomography detector: micron resolution at half-centimetre scale. J. Synchrotron Radiat. 29, 505–514 (2022).

20.      Moore, S. K. Samsung and Omnivision Claim Smallest Camera Pixels. IEEE Spectrum https://spectrum.ieee.org/cmos-image-sensor-pixel (2022).

21.      Henke, B. L., Gullikson, E. M. & Davis, J. C. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50-30,000 eV, Z = 1-92. At. Data Nucl. Data Tables 54, 181–342 (1993).

22.      Tennant, D. Soft X-ray microscopy with a cryo scanning transmission X-ray microscope: I. Instrumentation, imaging and spectroscopy. J. Microsc. 197, 68–79 (2000).

23.      Diamond Light Source About Us. https://www.diamond.ac.uk/Home/About/ (2022).

24.      Gradl, R. et al. Propagation-based Phase-Contrast X-ray Imaging at a Compact Light Source. Sci. Rep. 7, 4908 (2017).

25.      Gunther, B. et al. The versatile X-ray beamline of the Munich Compact Light Source: design, instrumentation and applications. J. Synchrotron Radiat. 27, 1395–1414 (2020).

26.      Willmott, P. Synchrotron Physics. in An Introduction to Synchrotron Radiation 39–86 (2011). doi:https://doi.org/10.1002/9781119970958.ch3.

I am driven by the power of technological breakthroughs to make positive change for humanity. While I also take immense pleasure in the artistic/creative aspects of technology design, my motivation centers on helping people and on protecting the future of the human species. I am therefore interested in a wide array of contemporary challenges. As a synthetic biologist, I can capitalize on my field’s multidisciplinary nature to explore many distinct applications. It should be noted that, as just one person, my knowledge can only go so deep in so many areas. Furthermore, interdisciplinary projects are much more likely to succeed when experts from multiple fields work together. Because of this, I extensively leverage collaboration. I am sharing this list as a way of increasing my likelihood of connecting with potential collaborators over time and as a method of inspiring others to consider how they too might contribute to creating a bright future. I chose the featured image of a Martian-hued rendering of a group of Anasazi cliff dwellings as a symbolic tribute to the creative and culturally rich spirit of humanity, an homage to where we have come from, and a hopeful indication of where we might go in the future.

Affordable Gene Therapy Manufacturing

Many existing gene therapy delivery vehicles are extremely expensive to produce, so treatments are very costly for patients and not enough doses can be made to reach large populations. Novel manufacturing solutions are vital to scalably make existing vectors (esp. AAVs). I am also particularly interested in developing new types of vectors that can be manufactured inexpensively while still retaining the benefits of existing delivery systems. Here are some potential directions of interest.

• Synthetic biology methods for radically redesign of cellular platforms of virus production
• Novel inexpensively producible viral vectors.
• Hybrid nanoparticle-viral vectors that are easier to produce yet retain benefits of viruses (and perhaps feature additional advantages).
• Methods for production of DNA origami nanorobots.
• DNA origami tools to support viral capsid assembly and genome packaging, methods for making these tools cheaply enough to facilitate their purpose.

Antibacterial Resistance

In particular, I hope to combat high risk pathogens such as carbapenem-resistant Enterobacterales, carbapenem-resistant Acinetobacter, Clostridioides difficile, and drug-resistant Neisseria gonorrhoeae. Adaptability and rapid generation of new solutions will represent key qualities to keep up with resistance. Here are some potential directions of interest.

• Treatments based on engineered bacteria to combat the pathogenic bacteria.
• Rational design (nanobiotechnology focus) of phage therapies.
• Phage therapy production platforms for rapid generation of diverse therapeutic candidates
• Lysogenic phage therapies for widespread resistance shutdown and/or bactericide.
• Sentinel bacteria for detection and elimination of resistance in environment (esp. livestock and wastewater), bacterial conjugation for elimination of resistance in environment.
• Gene therapies which enhance the immune system to combat antibiotic resistant bacteria.
• Rapid inexpensive biomanufacturing tools for making vaccines, rapid vaccine discovery platforms.
• Affordable home diagnostics.

Biological Carbon Capture for Climate Change

The climate crisis threatens human and nonhuman life. Some of the detrimental effects of climate change are desertification, flooding, extreme weather events, ecosystem collapse, food shortages, and emergence of new pathogens. As a result, climate change will cause many millions of deaths if it continues unchecked. It should be noted that addressing climate change will necessitate both policy changes and technological solutions. Carbon capture represents a particularly promising route towards mitigating climate change yet is difficult to scale. Self-replicating biological carbon capture approaches should display much greater scalability, though they will come with risks that must be addressed prior to deployment. Here are some potential directions of interest.

• Develop genetically enhanced trees that more rapidly capture carbon.
• Develop genetically enhanced cyanobacteria (or algae) that more rapidly capture carbon.
• Design bacteriophage-based delivery systems to propagate genes in ocean cyanobacteria to enhance their carbon uptake.
• Engineer bacterial conjugation delivery systems in ocean cyanobacteria to propagate genes that enhance resistance to bacteriophages, thus rapidly increasing cyanobacterial population size and carbon capture capacity (this would require carefully balanced implementation to avoid unintended negative side effects).
• Develop computational models and experimental model systems to explore possible side effects of all of the above, find ways to counterbalance those side effects.

Connectomics Towards Whole-Brain Emulation

Mapping the human brain (connectomics) at nanoscale resolution would enable a series of unprecedented advances across basic and applied neuroscience. Connectomics has potential applications in bioinspired artificial intelligence, bioinspired robotics, neural protheses and brain-computer interfaces, and treatments for brain disease. Connectomes may also provide the foundational first step towards whole-brain emulation; that is, simulation of the mind (and body) in a computer with sufficient biological realism to accurately recapitulate behavior. Whole-brain emulation has applications as a platform for studying brain function and brain disease (but note that are possible ethical concerns around such platforms), as one of the necessary steps towards gradual replacement mind uploading, as a way of recreating the human mind in a nonbiological body to facilitate space colonization, and more. Here are some potential directions of interest.

• Synchrotron expansion x-ray microscopy as a route to mapping mammalian connectomes in reasonable timeframes (i.e. a few years of imaging as opposed to thousands or millions of years of imaging).
• Improved x-ray microscopy hardware along with new sample treatment methods to improve tissue stability as well as allow multicolor imaging and possibly barcodes for labeling.
• Construction of many compact light source devices to efficiently map brain tissue in parallel.

Gene Therapy for Aging

Aging affects everyone. It is marked by deterioration of health and eventual death. Treatments for aging would greatly improve the human condition by making people both healthier and longer lived. It should be noted that life extension only linearly affects population growth, whereas reproduction exponentially affects population growth, so concerns about life extension causing overpopulation are often exaggerated. As human longevity increases, its small contribution to population growth will likely be mitigated by parallel growth of technologies that improve human sustainability (e.g. vertical farms, cultured meat, renewable energy, space habitation, etc.) Gene therapy has great potential for extending human longevity and simultaneously improving overall global health. Here are some potential directions of interest.

• Develop multigenic gene delivery vectors to facilitate complex genetic interventions towards mitigating aging in the brain and elsewhere.
• Design tools to identify how multiple genetic changes may synergistically improve healthspan and longevity, develop gene therapies that implement these changes together.
• Engineer regulatory pathways by inserting genetic circuit loci which optimally modulate gene expression for improving healthspan and longevity.

Gene Therapy for Space Colonization

Extended periods of time in space, on the moon, on Mars, etc. expose astronauts to large amounts of radiation. Furthermore, this represents just one example of the many physiological issues encountered as a consequence of prolonged time in space. Future space colonization efforts could be severely jeopardized by human radiation exposure and other physiological issues. An important specific problem is that radiation can cause problems with human reproduction, which may hamper efforts to populate the moon and Mars. Here are some potential directions of interest.

• Insert genes derived from radiation-resistant organisms such as tardigrades and Deinococcus radiodurans.
• Enhance human DNA repair pathways by adding new genetic circuits and/or by altering gene regulation to bias towards repair.
• Design tools for studying how genetic changes influence bone tissue responses to microgravity.
• Develop multigenic gene delivery vectors to facilitate complex genetic interventions towards improving physiological responses to space.
• Develop delivery systems that can safely transduce most or all cells in the adult human body.

Horizontal Gene Drives to Repair Pollinator Insect Networks

Insect pollinators form a crucial part of global ecosystems, yet populations of these insects are declining. In particular, many species of bees contribute heavily to ecosystem health via pollination. Decline of insect populations is furthermore negatively affecting many crops, limiting food production across the world. Some of the more prominent factors specifically causing bee decline include spread of invasive Varroa mites that carry pathogens like the deformed wing virus and prevalence of toxic pesticides in the environment. Here are some potential directions of interest.

• Horizontal gene transfer could occur after seeding donor bacteria into insect gut microbiota may help protect insect pollinators in a scalable fashion.
• Developing engineered gut bacteria with conjugative plasmids which propagate genes to combat Varroa mites, genes to combat deformed wing virus, and/or genes to degrade pesticide toxins could help mitigate bee decline.

Infectious Disease Burden in Developing Countries

As ailments which cause some of the most widespread suffering, I am especially interested in combatting malaria, tuberculosis, and HIV. I hope to implement translational strategies for dissemination of solutions. Here are some potential directions of interest.

• Gene drives to prevent mosquitos from carrying pathogens.
• Inexpensive home diagnostics.
• Rapid inexpensive biomanufacturing of treatments.
• Thermostable treatments and vaccines.
• Inexpensive immune enhancement gene therapies.
• Rapid inexpensive biomanufacturing of vaccines.

Nanobiotechnology for Neural Interfaces and Neural Prostheses

Existing neural interfaces and neural prostheses mostly use microelectrode-based technologies for recording and stimulating neuronal tissues. But microelectrodes are invasive, usually cause inflammation and glial scarring, and lack spatial precision. Nanobiotechnology approaches may allow less invasive, less toxic, and more precise neural interfaces and prostheses. Here are some potential directions of interest.

• Polymersome (or similar) compartments which mimic neurons in their electrical response properties using embedded transmembrane proteins.
• Such compartments may transmit current along protein-based nanowires to external devices or to other parts of the brain.
• Develop gene therapies to deliver DNA encoding ultrasound-responsive ion channels, enabling spatially controllable neurostimulation
• Develop delivery system to transport gas vesicles into the brain, allowing spatial ultrasound activation of cargo release for drug or gene delivery. This may also have applications to certain kinds of neural interfaces.

Nanorobotics

Researchers have so far created only simple nanorobots. More advanced forms of nanotechnology would enable a wide range of new directions across medicine, manufacturing, agriculture, space, and more. Ideally, stronger nanorobots should possess (1) inexpensive mass producibility or self-replication capabilities, (2) ways of programming them to alter their responses to stimuli, and (3) automated locomotion. Here are some potential directions of interest.

• Develop highly programmable microorganism-based nanorobots, perhaps using a combination of minimal cell technology (make sure to minimize immunogenicity as part of this) and complex optogenetic systems to facilitate external programmability.
• Design dynamic DNA origami nanostructures which incorporate optically programmable logic systems inspired by digital circuits.
• Develop scalable manufacturing platforms for new nanorobotics designs.

Terraforming

The future of humankind depends on space colonization, yet Earth represents the only planet in our solar system where humans can survive unaided. Terraforming the moon and/or Mars would provide us with new habitable worlds. Unfortunately, terraforming these places will be an enormously difficult task. Here are some potential directions of interest.

• Seeding Mars with heavily engineered extremophile microorganisms might act as a first step towards creating a new habitable world. They could metabolize regolith and convert it to Earthlike atmospheric gases and other useful substances.
• A similar approach might work on the moon, but it would be much more difficult due to the even harsher environment and complete lack of atmosphere.
• Certain types of nanoparticles may facilitate atmospheric warming on Mars, so developing ways of further augmenting the effects of such nanoparticles may benefit terraforming efforts.
• Develop ways of extensively engineering mosslike microorganisms so that they grow directly on partially terraformed Mars or moon may provide an abundant food source for early colonists. With the vast amount of land available, it may even be possible to send such food back to Earth to ameliorate world hunger.

PDF version: Guide to the Structure and Function of the Adenovirus Capsid

For this guide, I will explain the fundamental biology of adenovirus capsid proteins with an emphasis on the context of gene therapy. While the guide is meant primarily for readers with an interest in applying adenovirus to gene therapy, it will not include much discussion of the techniques and technologies involved in engineering adenoviruses for such purposes. If you are interested in learning more about adenovirus engineering, you may enjoy my review paper “Synthetic Biology Approaches for Engineering Next-Generation Adenoviral Gene Therapies” [1]. Here, I will focus mostly on the capsid of human adenovirus serotype 5 (Ad5) since it is the most commonly used type of adenovirus employed in gene therapy research, but I will occasionally describe other types of adenoviruses when necessary. Many of the presented concepts remain the same or similar across other types of adenoviruses.

The adenovirus consists of an icosahedral protein capsid enclosing a double-stranded DNA (dsDNA) genome. It possesses 12 fiber proteins which protrude from the capsid and helps to facilitate cellular transduction. Adenoviruses are nonenveloped and approximately 90 nm in diameter (not including the fibers). The Ad5 genome is about 36 kb in size. Major capsid proteins of the adenovirus include the hexon, penton, and fiber. The minor capsid proteins are protein IIIa, protein VI, protein VIII, and protein IX. Inside the capsid, there are core proteins including protein V, protein VII, protein μ (also known as protein X), adenovirus proteinase (AVP), protein IVa2, and terminal protein (TP) [2]. There are also many proteins expressed during adenovirus infection which are not incorporated into mature capsids, including the E1A proteins (289R, 243R, 217R, 171R, and 55R), the E1B proteins (52k and 55k), the adenoviral DNA polymerase, and more [3].

Ad5’s genome contains a variety of transcriptional units which are expressed at different times during the viral life cycle [3]. The E1A, E1B, E2A, E2B, E3, and E4 transcriptional units are expressed early during cellular infection. Their proteins are involved in DNA replication, transcriptional regulation, and suppression of host immune responses. The L1, L2, L3, L4, and L5 transcriptional units are expressed later in the life cycle. Their products include most of the capsid proteins as well as other proteins involved in packaging and assembly. Each transcriptional unit can produce multiple mRNAs through the host’s alternative splicing machinery.

Major capsid proteins

Hexon

Adenovirus hexon represents the main structural component of the capsid. It is encoded as one of the products of the Ad5 L3 gene. Each capsid contains 240 trimers of the hexon protein (720 monomers) and each facet of the icosahedron consists of 12 trimers [4]. The lower part of each hexon monomer consists of two eight-stranded β barrels linked by a β-sheet. The eight-stranded β-barrels are known as jellyroll domains. In between the β-strands, long loops are present. These loops contain the seven hypervariable regions (HVRs) of the hexon, which differ in sequence composition between distinct adenovirus types. The loops form the upper portion of each hexon. HVR1 of Ad5 includes a 32-residue acidic loop which might be involved in neutralizing host defensins. The valley between the loop towers of Ad5 has been shown to interact with coagulation factors as well as to bind to the CD46 cellular receptor as an alternative cell entry mechanism.

Here, the structure of the Ad5 hexon trimer is shown from a side view and from a top view (PDB 1P30). All β-sheets are red, α-helices are cyan, and loops are magenta. Jellyroll domains are visible at the base of the side view and the HVR loops can be seen in the upper half of the side view. In the top view, the hexagonal shape of the hexon is clearly visible. The N- and C- termini are both located near the bottom of the hexon (adjacent to the inside of the virion). Some disordered regions are shown as dashed lines.

Penton

The 12 pentons serve to fill pentagonal gaps within the icosahedral capsid (which arise due to the geometry of the hexons) [4]. Penton is encoded as one of the products of the Ad5 L2 gene. Each penton also acts as a base onto which a fiber protein is anchored. Adenovirus pentons are pentamers, with each monomeric subunit consisting of a single jellyroll domain for the lower part and both a hypervariable loop and a variable loop at the top. In Ad5 and many other human adenoviruses, the penton hypervariable loop includes an RGD amino acid sequence. RGD is both an α_v integrin binding motif and is a target for adenovirus neutralization by the enteric defensin HD5. Importantly, the penton’s RGD motif is essential for cellular transduction into clathrin-coated pits [5]. RGD may also play some role in endosomal escape. The other penton variable loop (distinct from the hypervariable loop) is poorly understood from a functional standpoint. Both the hypervariable loop and the variable loop might serve as decent sites for sequence modification in the context of gene therapy vectors. The penton N-terminal domain consists of approximately 50 amino acid sequence which extends into the inside of the adenovirus virion. This sequence is mostly disordered except for the part nearest to the jellyroll domain (residues 37-51 in Ad5), which interacts with two copies of protein IIIa.

Here, the structure of the Ad5 penton is shown from side and top views (PDB 3IZO). Coloration is by subunit. In the side view, the intravirion N-terminal domains are visible at the bottom, the jellyroll domains can be seen as the groups of β-sheets in the middle, and the loops are present at the upper region. The top view clearly illustrates the pentagonal symmetry of the penton. It should be noted that, in this structure, some of the loops are missing due to the difficulty of reconstructing them at high resolution. Of special relevance here is that the loop with the RGD sequence should be located at the top of the penton (in the gap between the uppermost α-helix and a nearby loop which both terminate prematurely).

Fiber

Ad5’s 12 trimeric fibers are anchored onto the tops of the pentons [4]. They are encoded as a product of the L5 gene. These fibers initiate cellular transduction through binding of the knob domain to cellular receptors. The primary receptor for Ad5 is the coxsackievirus and adenovirus receptor (CAR). That said, it should be noted that Ad5’s fiber knob can also bind to alternative receptors such as vascular cell adhesion molecule 1 and heparan sulfate proteoglycans. For Ad5, the fiber is about 37 nm in length, but other adenoviruses can have shorter or longer fibers [6]. Fibers consist of an N-terminal tail domain, a shaft domain, and a C-terminal knob (also called head) domain [4]. The three N-terminal tails anchor into some of the clefts between penton monomers, likely via a hydrophobic ring region. The shaft consists of a structure known as a trimeric β-spiral. Shaft flexibility plays a role in cellular transduction by facilitating interaction of the penton with its integrin receptor after binding of the knob to CAR. Many adenovirus fibers are known to have hinges at the third β-repeat from the N-terminal tail domain [7]. These hinges arise from an insertion of a few extra amino acids within the third β-repeat which disrupts its structure and allows for it to flex. The C-terminal knob domain consists of an antiparallel β-sandwich and is responsible for trimerization of the fiber [4]. Its C-termini are oriented back towards the capsid of the adenovirus.

Here, part of the structure of an Ad2 fiber is shown from two perspective views (PDB 1QIU). Though there are structures of the Ad5 fiber components available, only the above Ad2 fiber structure has been assembled into a complex with and made publicly available. The Ad2 fiber is highly similar to the Ad5 fiber. Both Ad5 and Ad2 fibers have 22 β-repeats. Only a few β-repeats are included in the above structures, but that should be enough to grant an intuitive understanding of the general fiber organization.

Minor capsid proteins

Protein IX

Ad5 protein IX (pIX) is a 140 amino acid protein found nestled between hexons which confers greater thermostability to the capsid relative to mutants lacking pIX [4]. There are 240 copies of pIX in the capsid. It has an N-terminal domain, a rope domain, and a C-terminal domain. The N-terminal domains of three pIX monomers interlace to form a triskelion structure in the valleys between some of the hexons. The rope domain (also called linker domain) is often disordered and connects the N- and C-terminal domains. The C-terminal domain is an α-helix which forms a coiled-coil structure with the helices of other copies of pIX monomer. This coiled coil consists of four α-helices (three parallel and one antiparallel), each from a different pIX monomer. Four triskelions and three α-helix bundles are present in each icosahedral facet of the capsid. It should be noted that some of the triskelions take on slightly different structural features depending on which hexons they are associated with within a given facet [8]. Though all of the C-termini of pIX are exposed on the capsid surface, they can still be described as resting within crevices between hexons. Because of this, spacer peptides are usually necessary when engineering Ad5 pIX-fusions such that that the added protein is elevated out of the crevices [9].

Here, four copies of Ad5 pIX are shown interlacing among four hexons (top and side views) (PDB 6B1T). The C-terminal domain α-helical bundle of pIX is clearly visible. The N-terminal domain triskelion structures are not visible in these views. Hexons are portrayed in cool colors and the pIX copies are shown in magenta. Some disordered regions are shown as dashed lines.

Protein IIIa

The Ad5 protein IIIa (pIIIa) plays a structural role in stabilizing the capsid from the inside [4]. Five copies of pIIIa are found under each vertex of the Ad5 capsid. It is 585 amino acids in length, but only residues 7 to 300 have been structurally traced at high resolution. Its N-terminal domain connects the penton and the five adjacent hexons. (These are known as the peripentonal hexons. The peripentonal hexons plus the penton are collectively named the group-of-six or GOS) Its C-terminal domain binds protein VIII (another structural protein which will be discussed later). The traced part of the pIIIa structure consists of two globular domains connected by a long α-helix.

Above, traced parts of five pIIIa proteins are shown on the underside of a part of the Ad5 capsid (perspective is from the interior) (PDB 6B1T). Hexons are colored blue, the penton is colored yellow, and pIIIa is colored bright pink. The same structure is shown below from a side perspective.

Protein VI

Ad5 protein VI (pVI) starts out as 250 amino acids long but is cleaved by AVP at two sites, yielding multiple peptides [4]. The first site is after residue 33 and the second is after residue 239. The middle part contains a predicted amphipathic α-helix (residues 34-54) which inserts into host endosomal membrane. This alters the membrane’s curvature and helps facilitate lysis of the endosome, allowing the adenovirus to escape into the cytosol. The middle part also contains a domain (residues 109-143) which sometimes binds to the inner surface of the capsid in the cavities between certain hexons. The N-terminal peptide pVI_N also binds to cavities between hexons. It has been suggested that this affinity hides the first pVI cleavage site in these cavities, preventing release of the membrane lytic peptide. During intracellular trafficking, environmental changes may allow adenovirus protein VII (a core protein) to outcompete pVI for the binding sites between hexons, causing release of the membrane lytic peptide. Finally, the C-terminal peptide pVI_C is a cofactor which helps activate AVP. The pVI_C peptide binds covalently to AVP and slides along the adenoviral genome, using the DNA as a track to reach all of the substrates in the core and the inner capsid surface. There are approximately 360 copies of protein VI in the Ad5 virion. Unfortunately, high-resolution structural data on pVI are scarce due to its variable position in the adenovirus virion.

Protein VIII

Ad5’s protein VIII (pVIII) also contributes to structurally stabilizing the adenoviral capsid from the interior [4]. It starts as a 227-residue protein which is cleaved by AVP at three sites, yielding two large peptides and two small peptides. The two large peptides stay together and bind between hexons. Some pVIII copies wedge between pIIIa and the peripentonal hexons, helping to connect the peripentonal hexons to the next set of surrounding hexons. Some pVIII copies are located underneath the nine hexons on the middle face of each icosahedral facet (known as the group-of-nine or GON). An interesting aspect of pVIII-hexon interactions is that can pVIII can engage in β-sheet augmentation, where a β-strand from pVIII is incorporated into one of the jellyroll domains of a nearby hexon. Not much is known about the two smaller peptides from pVIII except that these peptides do not appear to bind the capsid in a symmetric fashion.

Here, the traced parts of pVIII (red) are shown interwoven into a piece of the Ad5 capsid from an interior perspective (PDB 6B1T). Hexons are shown in shades of blue, the penton is shown in yellow, and pIIIa is displayed in bright pink.

Core proteins which interact directly with the capsid

Protein V

Adenovirus protein V (pV) is a positively charged protein which can form heterodimers with the pVII core protein [4]. That said, pV exists in a dimer-monomer equilibirium, so the binding to pVII is often transient. There also are direct associations between pV and the pVI capsid protein. These associations between pVII, pV, and pVI likely act to bridge the adenovirus core with the adenovirus capsid. In addition, pV-pVII heterodimers might interact with core protein μ. Each virion contains about 150 copies of pV. Most of the copies of pV are released during the beginning of uncoating. Interestingly, pV is not essential for adenovirus capsid assembly.

Protein VII

Protein VII (pVII) is a positively charged protein which plays a central role in condensing the adenovirus genome to fit into the capsid [4]. It has many arginine residues which contribute to its positive charge. AVP cleaves pVII at residues 13 and 24. The resulting middle peptide (including amino acids 13 through 24) might compete with pVI for hexon binding sites during adenovirus assembly. As mentioned earlier, environmental changes during intracellular trafficking may allow pVII to outcompete pVI for their hexon binding sites, causing release of the membrane lytic peptide from pVI cleavage. Though pVII acts as a functional analogue of the histone, it does not share much structural similarity with histones and does not replace histones when introduced into the cellular nucleus [2]. During infection, the viral genomic DNA as complexed with pVII is imported through nuclear pores. While pVII is important for condensing the adenoviral genome, it is not strictly required for assembly and packaging. In addition, pVII functions in signaling for the suppression of host innate immune responses. It binds to high mobility group B (HMGB) protein 1, a factor which is normally released from cells exposed to inflammation and which acts as a danger signal for the immune system. The adenoviral pVII prevents release of HMGB protein 1 and thereby dampens innate immune responses. Finally, pVII helps to regulate the progression of various steps during adenovirus genome replication.

Conclusion

This guide has centered on explaining the structures and functions of the Ad5 capsid proteins as well as the core proteins which are involved in key structural interactions with the capsid proteins. But this is only the beginning of learning about adenovirus biology. As mentioned in the introductory section, there are other core proteins including protein μ, the adenovirus proteinase, protein IVa2, and terminal protein which primarily interact with the adenovirus genome. Furthermore, the complex life cycle of the adenovirus requires numerous replication and packaging proteins (as well as interesting interactions with host cells) not covered here. Despite the specific focus of this guide, I hope that it is helpful to the reader for gaining a better idea of how the adenovirus capsid works. Perhaps this text will even provide a valuable bedrock of understanding for interested readers who are working on Ad5 capsid engineering projects.

References

[1]     L. T. Collins and D. T. Curiel, “Synthetic Biology Approaches for Engineering Next-Generation Adenoviral Gene Therapies,” ACS Nano, Aug. 2021, doi: 10.1021/acsnano.1c04556.

[2]     S. Kulanayake and S. K. Tikoo, “Adenovirus Core Proteins: Structure and Function,” Viruses , vol. 13, no. 3. 2021, doi: 10.3390/v13030388.

[3]     Y. S. Ahi and S. K. Mittal, “Components of Adenovirus Genome Packaging,” Frontiers in Microbiology, vol. 7. p. 1503, 2016, [Online]. Available: https://www.frontiersin.org/article/10.3389/fmicb.2016.01503.

[4]     J. Gallardo, M. Pérez-Illana, N. Martín-González, and C. San Martín, “Adenovirus Structure: What Is New?,” International Journal of Molecular Sciences , vol. 22, no. 10. 2021, doi: 10.3390/ijms22105240.

[5]     W. C. Russell, “Adenoviruses: update on structure and function,” J. Gen. Virol., vol. 90, no. 1, pp. 1–20, 2009, doi: https://doi.org/10.1099/vir.0.003087-0.

[6]     E. Vigne et al., “Genetic manipulations of adenovirus type 5 fiber resulting in liver tropism attenuation,” Gene Ther., vol. 10, no. 2, pp. 153–162, 2003, doi: 10.1038/sj.gt.3301845.

[7]     S. A. Nicklin, E. Wu, G. R. Nemerow, and A. H. Baker, “The influence of adenovirus fiber structure and function on vector development for gene therapy,” Mol. Ther., vol. 12, no. 3, pp. 384–393, Sep. 2005, doi: 10.1016/j.ymthe.2005.05.008.

[8]     V. S. Reddy and G. R. Nemerow, “Structures and organization of adenovirus cement proteins provide insights into the role of capsid maturation in virus entry and infection,” Proc. Natl. Acad. Sci., vol. 111, no. 32, pp. 11715 LP – 11720, Aug. 2014, doi: 10.1073/pnas.1408462111.

[9]     J. Vellinga et al., “Spacers Increase the Accessibility of Peptide Ligands Linked to the Carboxyl Terminus of Adenovirus Minor Capsid Protein IX,” J. Virol., vol. 78, no. 7, pp. 3470 LP – 3479, Apr. 2004, doi: 10.1128/JVI.78.7.3470-3479.2004.