PDF version: Notes on Optics and Microscopy
Wave optics
The wave equation
Because light exhibits wave-particle duality, wave-based descriptions of light are often appropriate in optical physics, allowing the establishment of an electromagnetic theory of light.
As electric fields can be generated by time-varying magnetic fields and magnetic fields can be generated time-varying electric fields, electromagnetic waves are perpendicular oscillating waves of electric and magnetic fields that propagate through space. For lossless media, the E and B field waves are in phase.
By manipulating Maxwell’s equations of electromagnetism, two relatively concise vector expressions that describe the propagation of electric and magnetic fields in free space are found. Recall that the constants ε0 and μ0 are the permittivity and permeability of free space respectively.

Since an electromagnetic wave consists of perpendicular electric and magnetic waves that are in phase, light can be described using the wave equation (which is equivalent to the expressions above). Note that the speed of light c = (ε0μ0)-1/2. Electromagnetic waves represent solutions to the wave equation.

Either the electric or the magnetic field can used to represent the electromagnetic wave since they propagate with the same phase and direction. With the exception of the wave equation above, the electric field E will instead be used to represent both waves. Note that either the electric or magnetic field can be employed to compute amplitudes.
Solutions to the wave equation
Plane waves represent an important class of solutions to the wave equation. The parameter k is the wavevector (which points in the direction of the wave’s propagation) with a magnitude equal to the wavenumber 2π/λ. In a 1-dimensional system, the dot product k•r is replaced by kx. The parameter ω is the angular frequency 2πf and φ is a phase shift.

To simplify calculations, Euler’s formula can be used to convert the equation above into complex exponential form. Only the real part describes the wave as the real part corresponds to the cosine term.

Spherical waves are another useful solution to the wave equation (though they are an approximation and truly spherical waves cannot exist). Because of their geometry, the electric field of a spherical wave is only dependent on distance from the origin. As such, the equation for a spherical wave can be written as seen below with origin r0.

Gaussian beams are a solution to the wave equation that can be used to model light from lasers or light propagating through lenses. If a Gaussian beam propagates in the z direction, then from the perspective of the xy plane, it shows a Gaussian intensity distribution. For a Gaussian beam, the amplitude decays over the direction of propagation according to some function A(z), R(z) represents the radius of curvature of the wavefront, and w(z) is the radius of the wave on the xy plane at distance z from the emitter. Often these functions can be approximated as constants.


Intensity and energy of electromagnetic waves
The Poynting vector S is oriented in the direction of a wave’s propagation (assuming that the wave’s energy flows in the direction of its propagation).

The magnitude of the Poynting vector represents the power per unit area (W/m2) or intensity crossing a surface with a normal parallel to S. Note that this is an approximation since, according to a quantum mechanical description of electromagnetic waves, the energy should be quantized.
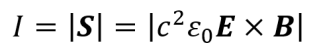
Power per unit area (intensity or irradiance) of plane waves, spherical waves, and Gaussian beams can also be calculated using the equations below. The formula for the Gaussian beam’s power represents the power at a plane perpendicular to the direction of light propagation z.

For electromagnetic waves, instantaneous energy per unit area is difficult to measure, so the average energy per unit area over a period of time Δt is often worked with instead. Since waves are continuous functions, taking their time-average requires an integral.

When using the above integral on the function eiωt, it is useful to think of finding the real and imaginary parts, cos(ωt) and sin(ωt). Then the time-averages of the cosine and sine functions can be computed using the following equations.

Polarization of light
The waves comprising linearly polarized light are all oriented at the same angle which is defined by the direction of the electric field of the light waves. For linearly polarized plane waves with electric fields oriented along the x or y axes that propagate in the z direction, the following equations describe their electric fields.

The superposition of two linearly polarized plane waves that are orthogonal to each other (and out of phase) is the vector sum of each electric field.

The superposition of two linearly polarized plane waves that are orthogonal to each other (and in phase) is computed via the following equation and has a tilt angle θ determined by the ratio of amplitudes of the original waves. This process can also be performed in reverse with a superposed polarized wave undergoing decomposition into two orthogonal waves.

When two constituent waves possess equal amplitudes and a phase shift of nπ/2, the superposed wave is circularly polarized (as it can be expressed using a sine and a cosine term). Equations for the constituent waves and the superposed wave are given below.
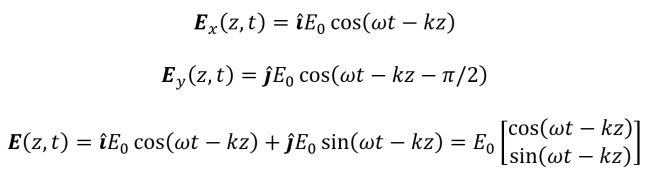

When circularly polarized light propagates, it takes a helical path and so rotates. As such, a full rotation occurs after one wavelength. If a circularly polarized wave rotates clockwise, it is called right-circularly polarized and has a positive sine term. If a circularly polarized wave rotates counterclockwise, it is called left-circularly polarized and has a negative sine term.
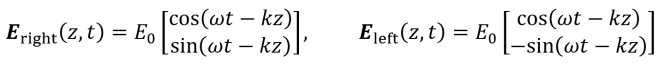
If a right-circularly polarized light wave and a left-circularly polarized light wave of equal amplitude are superposed, then they create a linearly polarized light wave with twice the amplitude of the individual waves.
![]()
Linearly polarized and circularly polarized light are special cases of elliptically polarized light. For elliptically polarized light, the amplitudes of the superposed waves may differ and the relative phase shift does not need to be nπ/2. As such, the electric field traces an elliptical helix as it propagates along the z direction.
![]()
For elliptically polarized light with a positive phase shift φ, it is called right-elliptically polarized if E0x > E0y and left-elliptically polarized if E0x < E0y.
Most light is unpolarized (or more appropriately, a mixture of randomly polarized waves). To obtain polarized light, polarizing filters are often used.
Superposition of waves with same frequency and direction
Let two waves E1 and E2 of the same frequency traveling in the same direction undergo superposition. E1 and E2 may or may not possess the same amplitude or phase. The substitution α = –(kx+φ) will be carried out.

If the phases of the waves are different, some special equations are necessary to find the amplitude E0 and the phase α of the resulting wave.

For the superposition of any number of these waves, the equations above can be extended.

It is often useful to employ complex exponentials when calculating the superposition of waves. For a sum of waves traveling in the same direction which all exhibit the same frequency, the following equation can be used. The summation in parentheses is called the complex amplitude of the resulting wave.

Superposition of waves with different frequencies
In another special case, consider calculation of the superposition of two waves with the same direction and amplitude E01 but different frequencies ω1 and ω2. The resulting wave can be expressed using the equation below. Since this wave takes on a beat pattern (see figure), the total disturbance of this wave has an average angular frequency (also called a temporal frequency) of ϖ = 0.5(ω1 + ω2) and an average propagation number (also called a spatial frequency) of k̅ = 0.5(k1 + k2). The quantity ωm is called the modulation frequency and the quantity km is called the modulation propagation number.


When waves of different frequencies undergo superposition, they create waves which themselves oscillate. The beat pattern is an example of this phenomenon. The smooth curves which outline the extremes of an oscillating signal are called the envelope of that signal.

Often when adding waves of different frequencies, the higher-frequency wave is referred to as the carrier wave and the lower-frequency wave is called the modulating wave. Since the modulating wave determines the envelope of the resulting waveform, this envelope is called the modulation envelope.
Furthermore, when waves of different frequencies undergo superposition, the modulation envelope travels at a different velocity than the constituent waves. The constituent waves travel at their phase velocities, given by v = ϖ/k̅, while the envelope travels at a group velocity. Note that in a nondispersive medium (vacuum), the phase and group velocities are the same since the speed of light is a constant. However, in a dispersive medium (non-vacuum), the phase velocity and group velocities differ. To find the group velocity, the equation below is used. If the frequencies of the two waves undergoing superposition are very similar, then the value of this formula approaches the derivative vg = dω/dk.

Superposition of waves using Fourier series
Fourier series can be utilized to represent periodic waves. To construct a Fourier series representation of a periodic function of a wave, the following equations are employed. As is consistent, λ is the wavelength and k is the wavenumber 2π/λ. More terms in a Fourier series representation leads to a more accurate approximation of the given wave.

It is often useful to create a Fourier series representation using complex exponentials. To do this, the following equations are used rather than those above.

Interference
Recall that the intensity (or irradiance) of an electromagnetic wave is the power received by a surface per unit area. Due to the high frequencies of many electromagnetic fields, it is often most useful to measure intensity. As such, equations for working with interference and intensity are valuable tools for optics.
When considering the interference of two waves with the same frequency E1(r,t) and E2(r,t), the average intensity Iavg of the resulting disturbance over a time period Δt is computed using the following equations. (This treatment assumes that the sources of the waves are separated by a distance much greater than their wavelength). To find Iavg at any given point in space, simply evaluate the equation for Iavg using the coordinates for that point. The angled brackets describe time averages over Δt (recall the integral from a previous section). Here, squaring a vector is equivalent to taking its dot product with itself.

In the case described above, the maximum intensity (total constructive interference) occurs where δ = 2nπ and the minimum intensity (total destructive interference) occurs where δ = (2n+1)π. The light and dark zones that result from constructive and destructive interference are called interference fringes.
For two waves to interfere, they must have the same or very close to the same frequency. In the case of a large frequency difference, a rapidly varying and time-dependent phase difference would occur, causing the interference term (E01•E02)cos(δ) to average to zero. However, when two sources emit white light, some interference takes place. This is because similar wavelengths within the white light will interfere with each other (e.g. blues will interfere with blues). For white light, the interference is not as sharp as in the case of monochromatic light.
Interference patterns will occur when any phase difference between the waves is constant. (Note that two waves with the same frequency and a constant phase difference are coherent waves). In addition, interference patterns are more clearly observable when the interfering waves have very similar amplitudes since this means that the maxima and minima of the interference fringes correspond to total constructive and total destructive interference.
Polarization of light can influence interference. Recall that the polarization state of a wave is defined by the orientation of its electric field. Even if coherent, two waves with orthogonal polarization states cannot interfere. By contrast, coherent waves with parallel polarization states will interfere.
Diffraction
Diffraction occurs when light encounters an obstruction and a multitude of scattered waves result, causing interference patterns to emerge. The vector theory of diffraction is very complicated. But in many applications, one can use approximate scalar treatments of diffraction which are based on Huygens’s principle. When dealing with a viewing position that is close to the obstruction, Fresnel diffraction is used. When dealing with a viewing position that is far from the obstruction, Fraunhofer diffraction is employed.
According to Huygens’s principle, each point on a wavefront can be treated as a source of a secondary spherical wavelet and the envelope of these wavelets describes the new position of the wavefront. One illustrative result of this is that a plane wave passing through an infinitesimal pinhole in a barrier will produce a spherical wave on the other side of the wall. For larger apertures in a barrier, the emerging wave will be the sum of an infinite number of spherical waves originating at each point on the area of the aperture (see figure). It should be noted that the backward propagating part of the secondary wavelet envelope is not physically accurate and is largely ignored in this scalar approximation of diffraction.
For light propagating through an aperture of any shape, the Huygens-Fresnel integral describes the electric field at a point in space r located past the barrier. This integral is an infinite sum of spherical waves that emerge from each infinitesimal point covering the barrier’s aperture. The constant i/λ arises as an approximation of the influence of the angle of the wave arriving at the aperture relative to the aperture’s normal vector. The domain Σ over which integration takes place is the aperture’s area and r0 represents an infinitesimal surface element of the aperture dx0dy0 (with the flat barrier and its aperture described as an xy plane). Ei(x0,y0) is the complex amplitude of the incident wave at the point x0,y0 on the flat barrier’s xy coordinate system. Here, θ represents the angle of the vector r – r0 relative to the aperture’s normal vector. A transmission function f(x0,y0) can be included inside the integral to describe the effect of a partially translucent surface. For the case of a fully opaque barrier and a fully translucent aperture, f(x0,y0) is zero at all barrier points and one at all aperture points. For a system with a partially translucent barrier or aperture, f(x0,y0) is a complex quantity with magnitudes falling between zero and one. Recall that the magnitude of a complex quantity a + bi is defined as (a2 + b2)1/2. Though it is an approximation, the Huygens-Fresnel integral is still complicated enough that it is often computed numerically.
the barrier’s aperture. The constant i/λ arises as an approximation of the influence of the angle of the wave arriving at the aperture relative to the aperture’s normal vector. The domain Σ over which integration takes place is the aperture’s area and r0 represents an infinitesimal surface element of the aperture dx0dy0 (with the flat barrier and its aperture described as an xy plane). Ei(x0,y0) is the complex amplitude of the incident wave at the point x0,y0 on the flat barrier’s xy coordinate system. Here, θ represents the angle of the vector r – r0 relative to the aperture’s normal vector. A transmission function f(x0,y0) can be included inside the integral to describe the effect of a partially translucent surface. For the case of a fully opaque barrier and a fully translucent aperture, f(x0,y0) is zero at all barrier points and one at all aperture points. For a system with a partially translucent barrier or aperture, f(x0,y0) is a complex quantity with magnitudes falling between zero and one. Recall that the magnitude of a complex quantity a + bi is defined as (a2 + b2)1/2. Though it is an approximation, the Huygens-Fresnel integral is still complicated enough that it is often computed numerically.

The Fraunhofer approximation is employed when the aperture’s size is small relative to the distance to the observation point (such that the light is approximately a plane wave at this observation point). It should be noted that converging lenses can decrease the necessary distance for using the Fraunhofer approximation. Fraunhofer diffraction also assumes that the light source is far enough from the aperture that the incident light can be considered a plane wave. A useful property of the Fraunhofer diffraction integral is that it is mathematically equivalent to a 2D Fourier transform of the aperture’s transmission function f(x0,y0). The Fraunhofer diffraction integral equation is given as follows. Here, x0 and y0 are points on the plane of the aperture or barrier while r or x, y, and z represent points anywhere in space.

Ray optics
Refraction and total internal reflection
When light moves between materials with different refractive indices, the refracted ray’s angle changes relative to the incident ray’s angle, a process called refraction. The refractive index n of a material describes the rate of propagation of light within that material relative to vacuum (which has a refractive index of one).
For most media, the refractive index of a given material varies with the wavelength of the light as n(λ). The property of birefringence also occurs in some materials (and is especially common in crystals). Birefringence is when a material’s refractive index varies depending on the angle of light propagation or on the polarization state of the light.
Refraction is described by Snell’s law. Here, θ1 is the incident ray’s angle relative to the normal of the interface, θ2 is the refracted ray’s angle relative to the normal of  the interface, n1 is the index of refraction of the material in which the incident ray propagates, and n2 is the index of refraction of the material in which the refracted ray propagates. If n1 < n2, the refracted ray bends towards the normal of the interface. If n1 > n2, the refracted ray bends away from the normal of the interface. It should be noted that refraction (and reflection) can also be studied in the context of wave optics.
the interface, n1 is the index of refraction of the material in which the incident ray propagates, and n2 is the index of refraction of the material in which the refracted ray propagates. If n1 < n2, the refracted ray bends towards the normal of the interface. If n1 > n2, the refracted ray bends away from the normal of the interface. It should be noted that refraction (and reflection) can also be studied in the context of wave optics.
![]()

In total internal reflection, a ray of light is reflected from an interface between two media at the same angle as the angle it approached the interface from. Total internal reflection occurs when the incident ray is traveling from a medium with a higher refractive index to a medium with a lower refractive index and approaches from an angle relative to the normal of the interface greater than a value called the critical angle θc. The critical angle is computed using the following equation.

Basic ray tracing and lenses
Though ray optics itself represents an approximation and is not as accurate as wave optics, a further simplification called the paraxial approximation is often still useful in practice. For the paraxial approximation, the angles made by all rays with respect the system’s optical axis (e.g. the line perpendicular to a lens) are assumed to be small enough that θ ≈ sin(θ) ≈ tan(θ) and that cos(θ) ≈ 1. This means that Snell’s law simplifies to n1θ1 = n2θ2.
When working with thin lenses and the paraxial approximation, three rules for ray tracing can be applied. (1) All rays which pass through a focal point on one side of the lens bend as they pass through the lens so that they are parallel to the optical axis when they continue on the other side of the lens. (2) Any ray which passes through the center of a lens continues in the same direction and does not bend. (3) All rays which are parallel to each other (though not necessarily to the optical axis) on one side of a lens will bend as they move through the lens to focus upon a single point on the other side. The location of this point is at the intersection of the optical axis with a ray that both passes through the center of the lens and is part of the group of parallel rays.
The distance dobj from an object to the thin lens, the distance dimg from the thin lens to where object’s associated image forms, the focal length f of the thin lens, and the magnification M of the thin lens are related using the following equations. The negative value of magnification indicates that the orientation of the image is inverted relative to the object.

The focal length of a thin lens is computed using a simplified form of the lens maker’s equation. R1 is the radius of curvature for the side of the lens closest to the light source, R2 is the radius of curvature for the side of the lens furthest from the light source, and n is the refractive index of the material of the lens. Sign conventions for R1 and R2 are usually as follows. If the lens is convex, R1 is positive and R2 is negative. If the lens is concave, R1 is negative and R2 is positive.
source, R2 is the radius of curvature for the side of the lens furthest from the light source, and n is the refractive index of the material of the lens. Sign conventions for R1 and R2 are usually as follows. If the lens is convex, R1 is positive and R2 is negative. If the lens is concave, R1 is negative and R2 is positive.

For thicker lenses, the full lens maker’s equation is used and takes the following form. Here, d represents the thickness of the lens.

Ray transfer matrix analysis
To aid in the analysis of complicated optical systems, a matrix-based formalism is often employed. Ray transfer matrix analysis requires the paraxial approximation; small enough angles of incident rays relative to the optical axis that θ ≈ sin(θ) ≈ tan(θ) and that cos(θ) ≈ 1). As a result of the paraxial approximation, the equations involved in the propagation of light rays are linear and therefore can be described using matrices. As usual, the propagation direction of rays is conventionally represented as going from left to right.
In ray transfer matrix analysis, a given ray starts out at an angle θ1 with respect to the optical axis and at a height y1 relative to the optical axis. After passing through an optical element or a series of optical elements (an optical system), the ray has an angle θ2 with respect to the optical axis and a height y2 relative to the optical axis. The ray transfer matrix M (also called the ABCD matrix) helps to compute an output ray from an input ray using an equation of the following form.

The entries of the ray transfer matrix depend upon the components of the given optical system. To describe combinations of several successive optical components, several 2×2 ray transfer matrices are multiplied in the order of the components to give an overall ray transfer matrix. Below is a table of ray transfer matrices for some common optical components.

Fundamentals of Microscopy
Typical organization of a basic light microscope
Modern light microscopes typically employ an objective lens and a tube lens. These are called infinity-corrected microscopes. The objective lens collects light rays and refracts them so that they are parallel to each other. Next, the tube lens focuses these parallel rays onto a detector. The space where the rays are parallel between the objective lens and the tube lens is called infinity space. The magnification of this system is computed by the ratio of the focal lengths of the tube lens and objective lens.


If the microscope allows for direct observation by eye, an extra lens (the ocular lens) refracts the light from the tube lens so that the rays are once again parallel to each other. These parallel rays are subsequently focused onto the retina by the human eye’s lens. The magnification produced by the ocular lens and human eye is the focal length of the ocular lens divided by distance from the eye that the brain perceives the image is located (about 25 cm). Ocular lenses are usually designed to give an additional magnification factor of 10x.
Many microscopes use a detector to carry out imaging rather than (or in addition to) direct observation by eye. Since detectors convert light into an array of pixels using a photodetector array, the size of the individual photodetector devices determines the maximum level of detail that the microscope can acquire. Smaller photodetectors allow for more detail, though this only helps if the microscope’s optics can achieve sufficient resolution to provide this level of detail in the first place.
Microscopes also require a light source to illuminate the sample. Light sources often pass light through the sample from beneath, though sometimes inverted configurations where the light source is at the top and the objective lens is underneath are used. To focus the light from a source onto a specimen, a condenser lens is employed. In addition, a component called the condenser diaphragm acts as an iris that can adjust the numerical aperture (a concept described in the next section) of the condenser lens by limiting the size of the light cone.
Resolution in light microscopy
The maximum angle at which rays from the specimen can be collected by the objective lens is called the angular aperture. Using the angular aperture, the numerical aperture NA of the objective lens is computed. Numerical aperture is important for calculating the resolution of a light microscope. Here, n is the refractive index of the medium between the lens and the specimen and α is half of the angular aperture.
![]()
The resolution of light microscopy is diffraction limited (except in super-resolution microscopy), meaning that diffractive effects result in a maximum achievable resolution which depends on wavelength and numerical aperture. To understand this, consider diffraction from a point object. (Assume small angles with respect to the optical axis and neglect vector analysis). According to Huygens’s principle, the point object diffracts incoming light into a spherical wave. Part of this spherical wave is converted into a plane wave by the objective lens. Next, the tube lens focuses this light. At the focus on the image plane, the waves constructively interfere since they exhibit the same optical pathlength. But around this point, the optical pathlengths are different and a series of concentric circles of destructive and constructive interference occur. This phenomenon is called the Airy pattern.
which depends on wavelength and numerical aperture. To understand this, consider diffraction from a point object. (Assume small angles with respect to the optical axis and neglect vector analysis). According to Huygens’s principle, the point object diffracts incoming light into a spherical wave. Part of this spherical wave is converted into a plane wave by the objective lens. Next, the tube lens focuses this light. At the focus on the image plane, the waves constructively interfere since they exhibit the same optical pathlength. But around this point, the optical pathlengths are different and a series of concentric circles of destructive and constructive interference occur. This phenomenon is called the Airy pattern.
The intensity of light from the Airy pattern is a type of point spread function (PSF). Any microscope image is made up of a tapestry of PSFs. It should be noted that the Airy pattern represents an ideal PSF for a perfect optical system and that many other kinds of PSF exist. By using the Fraunhofer diffraction integral and integrating over a circular aperture (the objective lens) with radius a, the Airy pattern’s field is calculated as a function of the angle θ between the optical axis and the line from the center of the aperture to the observation point (see the figure in the diffraction section for a visual depiction of θ). The function for the Airy pattern’s intensity can be computed by squaring the equation of the field. Here, J1 represents a type of function called a Bessel function of the first kind of order one. I0 is the maximum intensity at the Airy pattern’s center.
pattern represents an ideal PSF for a perfect optical system and that many other kinds of PSF exist. By using the Fraunhofer diffraction integral and integrating over a circular aperture (the objective lens) with radius a, the Airy pattern’s field is calculated as a function of the angle θ between the optical axis and the line from the center of the aperture to the observation point (see the figure in the diffraction section for a visual depiction of θ). The function for the Airy pattern’s intensity can be computed by squaring the equation of the field. Here, J1 represents a type of function called a Bessel function of the first kind of order one. I0 is the maximum intensity at the Airy pattern’s center.

The reason the Fraunhofer integral can be used is that the refraction of the spherical wave into a plane wave makes the component waves parallel such that the image plane is effectively at the far field. Also note that the radial symmetry of the Airy pattern allows for I(θ) to describe the pattern in 3D despite only depending on a single variable.
Since microscope images are made up of a tapestry of PSFs as mentioned above, PSFs are useful in helping to describe resolution. As a type of PSF, the Airy pattern is often used to help calculate resolution. The circular region of the Airy pattern with a radius defined by the distance between the intensity distribution’s central maximum and its first zero is called the Airy disk.
If two point objects are farther from each other than the radius of the Airy disk dR (which depends on wavelength and numerical aperture, they are perceivable as separate objects. This principle is used as a measure of lateral resolution (x and y directions) and is called the Rayleigh criterion. Note that there are also other measures of lateral resolution such as the Sparrow limit.
separate objects. This principle is used as a measure of lateral resolution (x and y directions) and is called the Rayleigh criterion. Note that there are also other measures of lateral resolution such as the Sparrow limit.
When the light source illuminating the object uses coherent light (where waves exhibit the same frequency and a constant phase difference), the Rayleigh criterion is given by the following equation. Laser-based light sources and situations in which the condenser aperture is closed to produce a pointlike light source are the most common type of coherent light sources used in microscopy. In the case of the narrow condenser aperture, the numerical aperture of the condenser is sometimes approximated as zero.

In the cases where incoherent light is involved, the situation is different since the light between two adjacent points does not interfere. This happens when the sample itself emits light (as in fluorescence microscopy) or when the numerical aperture of the condenser lens is greater than or equal to the numerical aperture of the objective lens, the Rayleigh criterion is given by the following equation.

Measuring axial resolution in a manner that is consistent with the Rayleigh criterion requires using the intensity distribution of light along the optical axis (z direction). This axial interference pattern is typically hourglass shaped. However, it still exhibits a central maximum as well as regions of minimum intensity along the z axis. The distance between the central maximum and the first minimum is used as an approximate measure of axial resolution. This distance can be computed using the following equation. Here, n is the refractive index of the immersion medium between the specimen and the objective lens.

As mentioned earlier, the size of the individual photodetector elements in a microscope’s detector array determines the maximum possible level of image detail. To collect all of the available information from an image, the size dd of each photodetector element must be at most half the resolution or radius dR of the Airy disk in the image plane (that is, dd ≤ dR/2). Because the microscope’s magnification makes the specimen appear larger, it also multiplies the apparent radius of each Airy disk. This means that a higher magnification factor will cause each Airy disk to cover a larger number of photodetector elements (and pixels). As such, the minimum magnification factor necessary to make it so that dd ≤ dR/2 is given by the following equation.


Lens aberrations
Because the refractive index of a lens is wavelength dependent, different colors of light passing through the lens refract at different angles and create distinct focal planes. This causes lens aberrations that are known as chromatic aberrations.
causes lens aberrations that are known as chromatic aberrations.
Most lenses have spherical curvature since lenses with other types of curves are much more difficult to manufacture. Note that this does not necessarily mean these lenses are entirely spherical, just that the curved surfaces on the lenses could act as parts of a sphere. Unfortunately, light refracts at different angles towards the edges of these kinds of lenses. This is a result of the angle of incidence for parallel rays changing with the increasing curvature near the edges. With different angles of refraction, distinct focal planes occur, producing lens aberrations called spherical aberrations.
Any curved lens does not produce a flat focal plane, but rather a bowl-shaped focal region. Since microscopy often involves imaging samples with mostly flat geometry (e.g. samples on glass slides), this bowl-shaped focal region leads to a type of aberration known as a field curvature aberration.
When there is a disparity between the focal distances of rays passing through the vertical and axis of a lens and the horizontal axis of the lens, it leads to poorer image quality, focuses point objects as streaks, and is called astigmatism. This aberration sometimes comes from differences in vertical curvature and horizontal curvature of a lens due to imperfections in manufacturing. But even in a lens with perfect symmetry, when the object under observation is located away from the optical axis, a form of astigmatism called oblique astigmatism can occur (which has the same effect of creating distinct focal planes for the horizontal and vertical axes of the lens). The further the object is from the optical axis, the more severe the oblique astigmatism.
Slightly tilted lenses can result in an aberration known as coma. With coma, a cometlike blur oriented either away from the optical axis (positive coma) or towards the optical axis (negative coma) occurs.
Types of objective lenses
To correct for chromatic aberrations which arise between two wavelengths of light (usually blue and red), compound lenses made from materials with different dispersion properties are used. These lenses are called achromatic lenses (or achromats) . Dispersion refers to the wavelength dependence of refractive index. Achromatic objective lenses typically employ convex lenses made from crown glass fused to concave lenses made from flint glass, though the entire objective often involves more than just this lens doublet. The differences in dispersion (and therefore refraction) resulting from the crown glass and flint glass cancel each other out, correcting for chromatic aberrations in two wavelengths and creating a single focal plane for both of these wavelengths of light. In addition, achromatic objectives correct for spherical aberrations in a single wavelength which lies between two chromatically corrected wavelengths.
. Dispersion refers to the wavelength dependence of refractive index. Achromatic objective lenses typically employ convex lenses made from crown glass fused to concave lenses made from flint glass, though the entire objective often involves more than just this lens doublet. The differences in dispersion (and therefore refraction) resulting from the crown glass and flint glass cancel each other out, correcting for chromatic aberrations in two wavelengths and creating a single focal plane for both of these wavelengths of light. In addition, achromatic objectives correct for spherical aberrations in a single wavelength which lies between two chromatically corrected wavelengths.
When correcting for chromatic aberrations between blue, red, and green wavelengths, a fluorite lens is often employed. Fluorite objectives are typically similar to achromatic objectives (in that they include fused convex and concave lenses), but they use convex lenses made from fluorite glass rather than flint glass. Though usually more expensive than achromats, the dispersion properties of the convex fluorite glass is better able to complement the material of the concave lens, leading to a single focal plane for red, blue, and green light.
Apochromatic objectives are very expensive and combine many individual lenses so as to correct for chromatic aberrations in four or even five wavelengths such as red, green, blue, near-UV, and near-infrared. They are also typically corrected for spherical aberration in green and blue wavelengths. Some apochromatic objectives are constructed to exhibit minimal field curvature and are called plan-apochromats.
There are also special objective lens designs for various applications. Some examples include long working distance objective lenses, immersion objectives (immersion of an objective in liquid often creates a closer refractive index match to the lens material and improves image quality), and UV-transparent objectives to support uses that involve ultraviolet light.
Mirrors
Many optical microscopy setups are complicated and require mirrors to direct light to the necessary locations. Mirrors are also used for many other purposes in microscopy (e.g. curved mirrors can spread light out, etc.) Reflectance, the ratio of reflected light to incident light, is used to quantitatively evaluate the performance of mirrors. The angle at which a ray of light undergoes reflection is equal to the incident ray’s angle relative to the normal of the mirror’s surface. The reflected ray travels away from the mirror on the opposite side of the normal.
Metallic mirrors are made by coating a substrate with a thin layer of metal. The electrons in metallic substances are not bound to any one atom, so they are free to move through a metal’s volume. As such, metals electromagnetic fields induce oscillations in these free electrons. The oscillations cause reemission of the wave with a 180° phase shift relative to the incident wave, leading to destructive interference along the direction of the incident wave’s propagation. Due to the destructive interference, the reflected wave does not transmit into the metal, only out from the surface.
Many metallic mirrors can achieve 90-95% reflectance depending on what material they are made from. However, there are tradeoffs since a metallic mirror’s reflectance can rapidly decrease outside of a certain wavelength range. For instance, silver shows around 95% reflectance across visible and infrared spectra but drastically lower reflectivity in the ultraviolet region. The reflectance R of a metallic mirror can be computed (as a proportion) using the equation below where n is the metallic coating’s refractive index and ε is the metallic coating’s molar extinction coefficient. The molar extinction coefficient is a measure of how strongly a material attenuates light at a given wavelength.

It should also be noted that the molar extinction coefficient can be found experimentally by using absorption spectroscopy and applying the Beer-Lambert law. The Beer-Lambert law is given below where L is the optical pathlength (the distance that light travels from one side of the sample to the other side), c is the molar concentration of the substance, and A is the measured absorbance.
![]()
Dielectric mirrors take advantage of the fact that nonmetallic materials exhibit some reflectivity. To make a dielectric mirror, alternating layers of materials with low and high refractive indices are deposited on top of a substrate. Partial reflection occurs at the interfaces between the layers. Because the many layers each contribute some reflection, the total reflectance of a dielectric mirror can exceed 99%. Dielectric mirrors are often used with laser sources.
used with laser sources.
For a dielectric mirror, the thicknesses and refractive indices of its layers allow tuning of the mirror’s properties. Some designs can reflect only a narrow range of wavelengths while others can reflect a broad range of wavelengths.
Dielectric mirrors that reflect a specific wavelength (or range of wavelengths) are often designed such that the thickness times the refractive index of each layer equals one quarter of the target wavelength. Layers with alternating low and high refractive indices are still used, so the thicknesses are varied accordingly. As a result, constructive interference occurs among the partially reflected waves at the interfaces between each layer, adding up to achieve a high level of reflectance. It should be noted that dielectric mirrors are sensitive to the angle of incidence and therefore require correct positioning to function properly.
One useful type of dielectric mirror is a dichroic mirror. These dichroic mirrors reflect a designated range of wavelengths and transmit colors (through the mirror) which fall outside of this range. To do this, the thicknesses and refractive indices of the layers are adjusted so as to cause constructive interference which reinforces wavelengths that fall within the desired range.
Though mirrors are often flat, curved mirrors are also common in microscopy. They are used to bend the paths taken by light, for focusing light, to magnify or reduce images, and other applications. Curved mirrors come in a variety of shapes (e.g. with spherical, parabolic, or hyperbolic curvature) and can have concave or convex geometry.
Curved mirrors can behave similarly to lenses, reflecting light rays to converge at a certain focal distance f. As a result, the mirror equations are identical to the thin lens equations (see below). Recall that this assumes the paraxial approximation. When the object or image is in front of the mirror the value of dobj or dimg is positive. When the object or image is behind the mirror the value of dobj or dimg is negative. Using these sign conventions along with ray tracing methods, the mirror equation can be applied to both concave and convex mirrors.

There are several useful concepts to note with regards to the properties of particular types of curved mirrors. Spherical mirrors have a focal length equal to half the radius of curvature. Concave cylindrical mirrors reflect light into a linear focal plane. Concave paraboloidal mirrors focus plane waves into a point source and can also convert a point source into a plane wave.
Sources
For fluorescence microscopes, there are usually two light sources. One is a standard halogen lamp that allows a user to view the specimen using light transmission rather than fluorescence. The other is a more specialized and much brighter light source used for exciting fluorophores, sometimes a mercury arc lamp, a xenon arc lamp, a metal halide lamp, or a laser source.
Mercury arc lamps, xenon arc lamps, and metal halide lamps emit light across a wide range of spectra, though they each exhibit some specific differences in their emission ranges and peaks as seen in the following figure. It should be noted that metal halide lamps have a longer lifetime than mercury arc lamps and xenon arc lamps. Unfortunately, these types of light source do not emit light with constant intensity in space and time. Photons undergo emission in bunches rather than in a uniform series, fluctuations in the lamp’s temperature and in the lamp’s electric current can cause emission inhomogeneities, and external electric fields can interfere with the uniformity of emission. These issues can sometimes cause problems in quantitative microscopy.

Lasers provide more stable illumination. Lasers that emit single wavelengths as well as lasers that emit a broad spectrum of wavelengths are available. Lasers use a process called stimulated emission to produce light. Stimulated emission involves external electromagnetic radiation causing excited electrons to transition to their ground states more frequently than they would otherwise, causing emission of photons. An important property of stimulated emission is that the emitted photons exhibit the same direction, frequency, phase, and polarization as the incident electromagnetic radiation.
References
Boudoux, C. (2017). Fundamentals of Biomedical Optics. Blurb, Incorporated.
Degiorgio, V., & Cristiani, I. (2015). Photonics: A Short Course. Springer International Publishing.
Guenther, R. D. (2019). Modern Optics Simplified. Oxford University Press.
Hecht, E. (2017). Optics. Pearson Education, Incorporated.
Kubitscheck, U. (2017). Fluorescence Microscopy: From Principles to Biological Applications. Wiley.
Murphy, D. B., & Davidson, M. W. (2012). Fundamentals of Light Microscopy and Electronic Imaging. Wiley.
Cover image source: Nature
One Comment