PDF version: Notes on Graph Theory – Logan Thrasher Collins

Definitions [1]

General Properties 1.1

• 1.1.1 Order: number of vertices in a graph.
• 1.1.2 Size: number of edges in a graph.
• 1.1.3 Trivial graph: a graph with exactly one vertex.
• 1.1.4 Nontrivial graph: a graph with an order of at least two.
• 1.1.5 Neighboring vertices: if e=uv is an edge of G, then u and v are joined by e and are neighbors. They are also called incident with each other.
• 1.1.6 Complete graph: a graph with the maximum possible size for a graph of order n. For a complete graph, every pair of vertices is adjacent.

Subgraphs 1.2

• 1.2.1 Subgraph: consider a graph G, a subset of its vertices V(H)⊆V(G), and a subset of its edges E(H)⊆E(G). The graph H is a subgraph of G.
• 1.2.2 Proper subgraph: consider a subgraph H⊆G. If G contains at least one vertex or edge not in H, then H is a proper subgraph of G.
• 1.2.3 Spanning subgraph: a subgraph H⊆G with the same vertex set as G.
• 1.2.4 Induced subgraph: a subgraph H⊆G which possesses the same edges as G, but only for the vertices V(H)⊆V(G), which might not be the full vertex set of the graph G.
• 1.2.5 Clique: a subgraph H⊆G for which H is also a complete graph.

Traversing Graphs 1.3

• 1.3.1 Walk: a sequence of vertices starting with u∈G and ending with v∈G such that consecutive vertices are adjacent.
• 1.3.2 Closed walk: a walk for which u=v.
• 1.3.3 Open walk: a walk for which u≠v.
• 1.3.4 Length of a walk: the number of edges traversed in a walk.
• 1.3.5 Trivial walk: a walk with a length of zero.
• 1.3.6 Trail: a walk in which no edge is traversed more than once.
• 1.3.7 Path: a walk in which no vertex is traversed more than once.
• 1.3.8 Circuit: a closed trail with length L≥3.
• 1.3.9 Cycle: a circuit which does not repeat any vertices except for the first and last. An odd cycle is a cycle with an odd length, an even cycle is a cycle with an even length, and a k-cycle is a cycle of length k.
• 1.3.10 Distance: given vertices u and v, the distance d(u,v) is the smallest length of any u-v path in G. This path is called a geodesic.
• 1.3.11 Diameter: the diameter diam(G) is the greatest distance between any pair of vertices in the connected graph G.
• 3.12 Face: a space enclosed by a cycle. The space outside of a graph is also defined as a face.

Connectedness 1.4

• 1.4.1 Connected vertices: if G contains a path from vertex u to vertex v, then u and v are connected vertices.
• 1.4.2 Connected graph: a graph for which every pair of vertices is connected.
• 1.4.3 Disconnected graph: a graph which is not a connected graph.
• 1.4.4 Component: a connected subgraph of G which is not a proper subgraph of any other subgraph of G. Alternatively, this is a connected subgraph H⊆G (connected within itself) which is not connected to any other subgraph in G.

Common Types of Graphs 1.5

• 1.5.1 Empty graph: a graph with n vertices and no edges.
• 1.5.2 Bipartite graph: a graph for which the vertex sets of G can be partitioned into two subsets U and W (called partite sets), such that every edge connects a vertex of U to a vertex of W. Note that this does not mean every vertex of U is adjacent to a vertex of W.
• 1.5.3 Complete bipartite graph: a bipartite graph for which vertex of U is adjacent to a vertex of W. This type of graph is denoted as K_s,t, where s and t represent the number of vertices in the sets U and W respectively.
• 1.5.4 Star: a complete bipartite graph for which either s=1 or t=1.
• 1.5.5 Multipartite graph: a graph for which V(G) can be partitioned into k subsets such that, for every edge uv∈G, the vertices u and v belong to different partite sets. This does not mean that every vertex of a given partite set is adjacent to a vertex from another partite set. Multipartite graphs are also called k-partite graphs.
• 1.5.6 Complete multipartite graph: a multipartite graph for which every vertex of a given partite set of the graph is adjacent to a vertex of another partite set of the graph.
• 1.5.7 Multigraph: in a multigraph, more than one edge is allowed between any given pair of vertices (multi-edges).
• 1.5.8 Pseudograph: a multigraph which allows one or more edges which joins a given vertex to itself (a loop or self-edge).
• 1.5.9 Weighted graph: a multigraph in which all multi-edges are replaced by single edges equipped with weights. The values of the weights are defined as the number of multi-edges between a given pair of vertices.
• 1.5.10 Digraph: a set of vertices together with a set of edges defined by ordered pairs of vertices (called directed edges or arcs). Given a directed edge (u,v), the vertex u is called adjacent to v and the vertex v is called adjacent from u. The vertices u and v are also said to be incident with the directed edge (u,v).
• 1.5.11 Oriented graph: a digraph without any pairs of vertices u and v connected by an equal number of edges with opposite directions.
• 1.5.12 Simple Graph: an undirected graph with no self-edges.

Operations on Graphs 1.6

• 1.6.1 Complement: a graph’s complement Ḡ possesses the same vertices as G, but has an edge uv if and only if uv is not an edge of G.
• 1.6.2 Union: given two graphs G and A, their union G∪A creates a disconnected graph 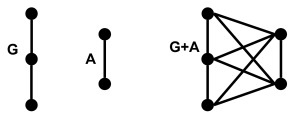with a vertex set V(G)∪V(A) and an edge set V(G)∪V(A).
• 1.6.3 Join: given two graph G and A, their join G+A creates the union of the graphs with the added property that each vertex of G is adjacent to all the vertices of A and each vertex of A is adjacent to all the vertices of G (as such, G+A is a connected graph).
• 1.6.4 Cartesian product: given two graphs G and A, their Cartesian product G⨯A has a vertex set for which every vertex of G⨯A is an ordered pair (u,v) where u∈V(G) and v∈V(A). Two distinct vertices (u,v) and (s,t) within G⨯A are adjacent if either u=s and vt∈E(H) or v=t and us∈E(G). Note that this method of constructing G⨯A requires the vertices of G and A to be labeled in a sequential manner (i.e. V(G)={g₁,g₂,…,g_n} and V(A)={a₁,a₂,…,a_m}) so that equivalences between vertices can be decided. In addition, the Cartesian product of graphs is commutative, that is G⨯A=A⨯G.
• 1.6.5 Transpose: given a digraph D, its transpose is the digraph R such that the direction of each arc in D is reversed.

Definitions [2]

Degrees 2.1

• 2.1.1 Degree: the number of edges incident with a vertex v. This is equivalent to the number of vertices adjacent to v. The degree of v is often denoted as deg(v).
• 2.1.2 Neighborhood: the set N(v) of vertices adjacent to a vertex v.
• 2.1.3 Isolated vertex: a vertex with a degree of zero.
• 2.1.4 Leaf: a vertex with a degree of one, also called an end-vertex.
• 2.1.5 Minimum degree: given a graph G, its minimum degree δ(G) is the lowest degree among the vertices of G.
• 2.1.6 Maximum degree: given a graph G, its maximum degree Δ(G) is the highest degree among the vertices of G.
• 2.1.7 Even vertex: a vertex of even degree.
• 2.1.8 Odd vertex: a vertex of odd degree.
• 2.1.9 Outdegree: for a digraph D, the outdegree od(v) is the number of vertices of D to which v is adjacent.
• 2.1.10 Indegree: for a digraph D, the indegree id(v) is the number of vertices of D from which v is adjacent.
• 2.1.11 Regular graph: a graph with δ(G)=Δ(G) is called regular. For regular graphs, all vertices have the same degree. The degree r of a regular graph’s vertices is used to classify the graph as r-regular.
• 2.1.12 Cubic graph: a graph which is 3-regular.
• 2.1.13 Degree sequence: any list of the degrees found in some graph. Usually, degree sequences can be ordered in multiple ways.
• 2.1.14 Graphical: a finite sequence of nonnegative integers is called graphical if it corresponds to some graph G.

Irregular Graphs 2.2

• 2.2.1 Irregular graph: a graph G with an order of at least two is called irregular if every pair of vertices u∈V(G) and v∈V(G) have distinct degrees.
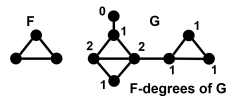
• 2.2.2 F-degree: for a nontrivial subgraph F⊆G and a vertex v∈G, the F-degree (denoted Fdeg) is the number of copies of F in G which contain v.
• 2.2.3 F-regular: a graph is F-regular if every pair of vertices has the same F-degree.
• 2.2.4 F-irregular: a graph is F-irregular if all pairs of vertices have distinct F-degrees.
• 2.2.5 Underlying graph: if all multi-edges in a multigraph M are replaced by single edges, the resulting graph is called the underlying graph of M.

Matrices and Edge Lists for Graphs 2.3

• 2.3.1 Adjacency matrix: given a graph G of order n, its adjacency matrix A=a_ij is the n x n matrix defined below. Adjacency matrices of simple graphs are symmetric with zeros along the diagonal. Adjacency matrices of pseudographs may have some ones on the diagonal (which indicates self-edges). Adjacency matrices of multigraphs may have integer values greater than one (which indicate more than one edge between given pairs of vertices). Adjacency matrices of digraphs (specifically oriented graphs) are not symmetric (indicating directed edges).

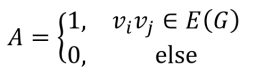
• 2.3.2 Incidence matrix: given a graph G of order n and size m, its incidence matrix B=b_ij is the n x m matrix defined below.

• 2.3.3 Edge list: a list of ordered pairs (u₁,v₁), (u₂,v₂), … , (u_n,u_n) which corresponds to all of the edges in a graph.

Definitions [3]

Isomorphic Graphs 3.1

• 3.1.1 Equal graphs: a pair of graphs with the same vertex set and edge set.
• 3.1.2 Isomorphic graphs: two graphs G and H are isomorphic if there exists a bijective function ϕ which maps V(G) to V(H) such that uv∈E(G) if and only if ϕ(u)ϕ(v)∈V(H). The bijective function ϕ is called an isomorphism. Isomorphic graphs are denoted as G≌H. Isomorphisms are also equivalence relations (and so possess the properties of equivalence relations). Note that isomorphic graphs possess the same structure, but might be drawn differently.
• 3.1.3 Isomorphic digraphs: digraphs D₁ and D₂ are isomorphic if there exists a bijective function ϕ which maps V(D₁) to V(D₂) such that the directed edge (u₁,v₁)∈E(D₁) if and only if (ϕ(u₁),ϕ(v₁))∈E(D₂).
• 3.1.4 Isomorphic to a subgraph: given unlabeled graphs G and H, if for any labeling of 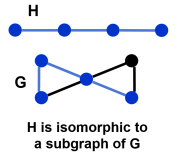the vertices of H and G, the labeled graph H is isomorphic to a subgraph of the labeled graph G.
• 3.1.5 Non-isomorphic graphs: graphs that are not isomorphic, denoted as G≇H.
• 3.1.6 Self-complementary: a graph G which is isomorphic with its complement Ḡ.

Trees 3.2

• 3.2.1 Bridge: consider an edge e=uv of a connected graph G. If removing e from G gives a disconnected graph, then e is a bridge.
• 3.2.2 Acyclic graph: a graph with no cycles. If an acyclic graph consists of more than one component, it is also called a forest.
• 3.2.3 Tree: an acyclic connected graph T.
• 3.2.4 End-vertex: a vertex with a degree of one.
• 3.2.5 Double star: a tree containing exactly two vertices that are not end-vertices.
• 3.2.6 Linear graph: a tree with exactly two end-vertices, also called a path graph.
• 3.2.7 Caterpillar: a tree with an order of at least three for which removal of its end-vertices would give a linear graph. In the case of caterpillars, this linear graph is called a spine.
• 3.2.8 Rooted tree: a tree T for which some vertex v∈T is designated as the root of T. When drawing rooted trees, the root is placed at the top and the other vertices at successively lower levels depending on their geodesic distance from the root.

Minimum Spanning Tree Problem 3.3

• 3.3.1 Spanning tree: given a connected graph G, a spanning tree is a spanning subgraph T⊆G that is also a tree.
• 3.3.2 Minimum spanning tree: given a connected weighted graph G, its minimum spanning tree is the spanning tree T for which the sum of its edge weights is the lowest value among all possible spanning trees of G. Finding a minimum spanning tree of a graph G is called the minimum spanning tree problem.
• 3.3.3 Kruskal’s algorithm: an algorithm for finding a minimum spanning tree T of a connected weighted graph G. To carry out Kruskal’s algorithm, first choose any edge e₁∈G with the minimum weight among the edge set of G and mark e₁ as an edge of T. Then choose another edge e₂∈G with the minimum weight among the remaining edge set of G and mark e₂ as an edge of T. Next, choose a third edge e₃∈G such that adding e₃ into the edge set of T does not create any cycles (e₃ must still possess the minimum weight among the remaining edge set of G) and mark e₃ as an edge of T. Continue this process with each new edge having the minimum weight among the remaining edge set and not creating any cycles until a spanning graph T has been constructed. The resulting graph is a minimum spanning tree of G.
• 3.3.4 Prim’s algorithm: an algorithm for finding a minimum spanning tree T of a connected weighted graph G with order n. To carry out Prim’s algorithm, first choose any vertex v∈G and an edge e₁∈G incident with v such that e₁ has the lowest weight among the edges incident with v. Add this edge to T. Continue adding edges (e₂, e₃, e₄, … , e_n-1) to T such that each edge has the minimum weight among the set of edges that possess exactly one vertex incident with an edge already selected.

Definitions [4]

Connectivity 4.1

• 4.1.1 Cut-vertex: given a connected graph G, if the removal of a vertex v∈G turns G into a disconnected graph, then v is called a cut-vertex. (Note that vertex removal can be denoted by G – v). For a disconnected graph G, cut-vertices are defined as vertices for which removal would turn any component of G into two or more disconnected subgraphs of G (rather than a single disconnected subgraph of G).
• 4.1.2 Nonseparable graph: a nontrivial connected graph which does not contain any cut-vertices.
• 4.1.3 Separable graph: a nontrivial connected graph which contains at least one cut-vertex.
• 4.1.4 Edge-disjoint subgraphs: two subgraphs are called edge-disjoint if they do not share any common edges.
• 4.1.5 Block: for a nontrivial connected graph G which is separable, a block is a nonseparable subgraph H⊆G such that H is not a proper subgraph of any other nonseparable subgraph in G.
• 4.1.6 Vertex-cut: a set of vertices U∈V(G) such that G – U is a disconnected graph.
• 4.1.7 Minimum vertex-cut: a vertex-cut of minimum cardinality in G (cardinality is the number of elements in a set).
• 4.1.8 Vertex-connectivity: the cardinality of a minimum vertex-cut of a graph. Vertex connectivity is also referred to as just connectivity and is denoted by κ(G).
• 4.1.9 k-connected graph: a graph with κ(G)≥k (where k is a nonnegative integer).
• 4.1.10 Edge-cut: a set of edges X∈E(G) such that G – X is a disconnected graph.
• 4.1.11 Minimal edge-cut: an edge-cut X of a connected graph G is called minimal if no proper subset of X is an edge-cut of G.
• 4.1.12 Minimum edge-cut: for an edge-cut X which is not minimal (of a connected graph G), there exists a proper subset Y⊂X that is a minimal edge edge-cut. An edge-cut of minimum cardinality is called a minimum edge-cut. Note that every minimum edge-cut is a minimal edge-cut, but not every minimal edge-cut is a minimum edge-cut.
• 4.1.13 Edge-connectivity: given a nontrivial graph G, the edge-connectivity λ(G) is the cardinality of a minimum edge-cut of G.
• 4.1.14 k-edge-connected graph: a graph with λ(G)≥k (where k is a nonnegative integer), often denoted by K_n.

Terms Relevant to Menger’s Theorem 4.2

• 4.2.1 Separation: a set of vertices S∈G separates two vertices u and v if G – S is a disconnected graph with u and v belonging to different components of G – S. The set S is called a u-v separating set.
• 4.2.2 Minimum u-v separating set: a u-v separating set S with minimum cardinality among all possible u-v separating sets of a graph.
• 4.2.3 Internal vertex: given a u-v path P, an internal vertex of P is a vertex w∈P such that w≠u,v.
• 4.2.4 Internally disjoint paths: a collection of u-v paths {P₁,P₂,…,P_k} such that none of the paths possess common vertices with the exception of the vertices u and v.

Definitions [5]

Eulerian Graphs 5.1

• 5.1.1 Eulerian circuit: a circuit which contains every edge of a graph G.
• 5.1.2 Eulerian graph: a connected graph containing an Eulerian circuit.
• 5.1.3 Eulerian trail: an open trail which contains every edge of a graph G.

Hamiltonian Graphs 5.2

• 5.2.1 Hamiltonian walk: a walk which contains every vertex of a graph G.
• 5.2.2 Hamiltonian cycle: a cycle which contains every vertex of a graph G.
• 5.2.3 Hamiltonian graph: a graph containing a Hamiltonian cycle.
• 5.2.4 Hamiltonian path: a path which contains every vertex of a graph G.
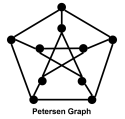
• 5.2.5 Petersen graph: a simple graph with ten vertices and fifteen edges, often used as a counterexample for various graph-theoretic problems.
• 5.2.6 Spanning walk: a walk which visits every vertex of a graph at least once. Note that a Hamiltonian walk is a closed spanning walk of minimum length.

Digraphs 5.3

• 5.3.1 Orientation of a graph: given a simple graph G, the orientation of G is a digraph generated by assigning a direction to each edge of G.
• 5.3.2 Subdigraph: a digraph H such that V(H)⊆G and E(H)⊆G where G is a digraph containing H.
• 5.3.3 Symmetric digraph: a digraph D for which every directed directed edge (u,v)∈G, there also exists a directed edge (v,u)∈G. Note that directed edges are also called arcs.
• 5.3.4 Directed walk: a sequence of vertices starting with u∈G and ending with v∈G such that consecutive vertices are adjacent and the walker proceeds in the direction of the arrows. The length of a directed walk is the number of arcs traversed. If no arc is repeated over a directed walk, then the directed walk is called a directed trail. If no vertex is repeated over a directed walk, then the directed walk is called a directed path.
• 5.3.5 Closed directed walk: a directed walk such that u=v.
• 5.3.6 Open directed walk: a directed walk such that u≠v.
• 5.3.7 Directed circuit: a closed directed trail with a length of at least two.
• 5.3.8 Directed cycle: a closed directed walk with a length of at least two.
• 5.3.9 Directed distance: given a digraph D and vertices u,v∈D, the directed distance d(u,v) is the length of the shortest u-v path in D. As with simple graphs, a u-v path of length d(u,v) is called a geodesic.
• 5.3.10 Weakly connected digraph: a digraph D with a connected underlying graph.
• 5.3.11 Strongly connected digraph: if a digraph D contains both a u-v path and a v-u path for every pair of vertices u,v∈D. An orientation which converts a simple graph into a strongly connected digraph is called a strong orientation. Alternatively, a strongly connected digraph is a digraph for which every vertex can be visited by a single directed path.
• 5.3.12 Eulerian digraph: a digraph containing an Eulerian circuit.

Digraph Tournaments 5.4

• 5.4.1 Tournament: an orientation of a complete graph.
• 5.4.2 Transitive tournament: a tournament T for which the following statement holds. Whenever T has arcs (u,v) and (v,w), it also has an arc (u,w).
• 5.4.3 Directed Hamiltonian path: a path containing all vertices of a digraph D.
• 5.4.4 Directed Hamiltonian cycle: a cycle containing all vertices of a digraph D.
• 5.4.5 Hamiltonian digraph: a digraph D containing a Hamiltonian cycle.

Theorems [1]

• Theorem 1.1: if a graph G with a walk of length L, then G contains a path of length p≤L.
• Theorem 1.2: the vertices and edges of a trail, path, circuit, or cycle in a graph G form a subgraph H⊆G.
• Theorem 1.3: if vertices u and v belong to different components of a disconnected graph, uv∉E(G).
• Theorem 1.4: given a graph G with an order of three or more and two distinct vertices u and v. If u is connected to G and v is connected to G, then G is a connected graph.
• Theorem 1.5: given a connected graph G with an order of three or more, G contains a pair of distinct vertices u and v such that G is connected to u and G is connected to v.
• Theorem 1.6: the size of a complete graph of order n is given by n(n-1)/2.
• Theorem 1.7: if G is a disconnected graph, then its complement Ḡ is connected.
• Theorem 1.8: the nontrivial graph G is a bipartite graph if and only if G does not contain odd cycles.

Theorems [2]

• Theorem 2.1 handshaking lemma: given a graph G with a size of m, the sum of the degrees of the vertices is equal to 2m (or twice the total number of edges).

• Theorem 2.2: every graph has an even number of odd vertices.
• Theorem 2.3: given a graph G of order n and the relation below (in which u and v represent nonadjacent vertices), G is connected and diam(G)≤2.

• Theorem 2.4: given a graph G of order n and δ(G)≥(n-1)/2, the graph G is connected.
• Theorem 2.5: given integers r and n such that 0≤r≤n-1, there exists an r-regular graph of order n if and only if either r or n is even.
• Theorem 2.6: for every graph H and every integer r≥Δ(G), there exists an r-regular graph G which contains H as an induced subgraph.
• Theorem 2.7: a non-increasing sequence of nonnegative integers s₁, s₂, … s_n (where s₁≥1) is graphical if and only if the sequence below is graphical.

• Theorem 2.8: if a graph’s adjacency matrix A=a_ij is raised to a power k, then the entry a_ij^k in row i and column j of A^k is equal to the number of distinct v_i-v_j walks of length k within the graph.
• Theorem 2.9 the party theorem: for any nontrivial simple graph, there exists a pair of vertices with the same degree. As such, no nontrivial simple graph is irregular.
• Theorem 2.10: given a graph F with order k≥2 and a graph G which contains m copies of F as subgraphs, the equality below (involving the F-degree) is true.

• Theorem 2.11: given a subgraph F with an even order and a graph G, the graph G has an even number of vertices with an odd F-degree.
• Theorem 2.12: given a nontrivial connected graph F, there exists an F-irregular graph if and only if Fdeg≠2.
• Theorem 2.13: given a connected graph G with an order of two or more, G is the underlying graph of an irregular multigraph or irregular weighted graph.
• Theorem 2.14 Euler’s formula: given a graph with V vertices, E edges, and F faces (recall that the space outside of a graph is counted as a face) that is drawn without edge intersections, the relation below is always true.

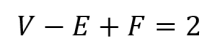
• Theorem 2.15: given an adjacency matrix A of a digraph D, the transposed matrix A^T is the adjacency matrix of a digraph R such that R is the graph transpose of D.

Theorems [3]

• Theorem 3.1: two graphs are isomorphic if and only if their complements are isomorphic.
• Theorem 3.2: two isomorphic graphs G and H possess identical sets of vertex degrees.
• Theorem 3.3: two isomorphic graphs G and H possess the same structural properties. For instance, G is bipartite if and only if H is bipartite, G is connected if and only if H is connected, G contains a 3-cycle if and only if H contains a 3-cycle, etc.
• Theorem 3.4: isomorphism is an equivalence relation on the set of all graphs and so isomorphism is reflexive (every graph is isomorphic to itself), symmetric (there exists an inverse for every isomorphism), and transitive (if G₁≌G₂ and G₂≌G₃, then G₁≌G₃).
• Theorem 3.5: an edge e∈G is a bridge if and only if e does not lie on any cycles of G.
• Theorem 3.6: a graph G is a tree if and only if every pair of vertices in G are connected by a unique path.
• Theorem 3.7: every nontrivial tree has at least two end-vertices.
• Theorem 3.8: every tree of order n has a size of n–1.
• Theorem 3.9: every forest of order n with k components has a size of n–k.
• Theorem 3.10: given a graph G of order n and size, if G satisfies any two of the following properties, then G is a tree. (i) G is connected, (ii) G is acyclic, (iii) m=n–1.
• Theorem 3.11: if T is a tree with order k and G is a graph with minimum degree δ(G)≥k–1, then T is isomorphic to some subgraph of G.
• Theorem 3.12: every connected graph contains at least one spanning tree.

Theorems [4]

• Theorem 4.1: given a vertex v incident with a bridge within a connected graph G, v is a cut-vertex of G if and only if deg(v)≥2.
• Theorem 4.2: given a connected graph G with an order of three or greater, if G contains a bridge, then G contains a cut-vertex.
• Theorem 4.3: given a cut-vertex v in a connected graph G as well as vertices u and w that belong to distinct components of the disconnected graph G – v, the vertex v lies on every u-w path of G.
• Theorem 4.4: a vertex v of a connected graph G is a cut-vertex if and only if there exist vertices u and w (distinct from v) such that v lies on every u-w path of G.
• Theorem 4.5: consider a nontrivial connected graph G and vertices u,v∈V(G). If v is the farthest possible vertex from u as measured by d(u,v), then v is not a cut-vertex of G.
• Theorem 4.6: every nontrivial connected graph contains at least two vertices which are not cut-vertices.
• Theorem 4.7: given a graph G with an order of three or greater, G is nonseparable if and only if every two vertices lie on a common cycle.
• Theorem 4.8: an equivalence relation R can be defined on the edge set of a nontrivial connected graph G for edges e,f∈E(G) when e=f or e and f lie on a common cycle of G.
• Theorem 4.9: every two distinct blocks B₁ and B₂ in a nontrivial connected graph have the following properties. (i) B₁ and B₂ are edge disjoint, (ii) B₁ and B₂ have at most one common vertex, and (iii) if B₁ and B₂ share a common vertex v, then v is a cut-vertex of G.
• Theorem 4.10: for every positive integer n, there exists a k-edge-connected graph K_n such that λ(K_n)=n-1.
• Theorem 4.11: for every graph G, the relation κ(G)≤λ(G)≤δ(G) holds. (Recall that δ(G) denotes a graph’s minimum degree).
• Theorem 4.12: for a cubic graph (3-regular), then κ(G)=λ(G).
• Theorem 4.13: if a graph has order n and size m≥n-1, then κ(G)≤2m/n.
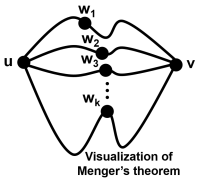
• Theorem 4.14 Menger’s theorem: given nonadjacent vertices u and v in a graph G, the minimum number of vertices in a u-v separating set equals the maximum number of internally disjoint u-v paths in G.
• Theorem 4.15: a nontrivial graph G is k-connected for an integer k≥2 if and only if every pair of distinct vertices u,v∈G corresponds to at least k internally disjoint u-v paths in G.
• Theorem 4.16: given a k-connected graph G any set S of k vertices in G, if a new vertex w is created and joined to the vertices of S, then the resulting graph is also k-connected.
• Theorem 4.17: given a k-connected graph G and vertices k+1 distinct vertices of u,v₁,v₂,…,v_k∈G; there exist internally disjoint u-v_i paths such that 1≤i≤k.
• Theorem 4.18: given a k-connected graph G with k≥2, every k vertices of G lie on a common cycle of G.
• Theorem 4.19: given distinct vertices u and v in a graph G, the minimum number of edges in G which separate u and v equals the maximum number of edge-disjoint u-v paths in G for each pair of distinct vertices u,v∈
• Theorem 4.20: a nontrivial graph G is k-edge-connected if and only if G contains k edge-disjoint u-v paths for each pair of distinct vertices u,v∈G.

Theorems [5]

• Theorem 5.1: a connected graph G contains an Eulerian trail if and only if every vertex of G has an even degree or exactly two vertices of G have odd degrees. In the case of a graph with exactly two vertices of odd degree, each Eulerian trail begins at one of the vertices with an odd degree and ends at the other vertex with an odd degree.
• Theorem 5.2: the Petersen graph is non-Hamiltonian.
• Theorem 5.3: given a Hamiltonian graph G, then every nonempty proper subset S of vertices in G satisfies the relation k(G – S)≤|S|, where k(G – S) is the number of components in the graph G – S and |S| is the cardinality of S.
• Theorem 5.4: if a graph G contains a cut-vertex, then G is not Hamiltonian.
• Theorem 5.5: given a graph G with an order n≥3, if deg(u)+deg(v)≥n for every pair of nonadjacent vertices u,v∈G, then G is Hamiltonian.
• Theorem 5.6: given a graph G with an order n≥3 and deg(v)≥n/2 for every vertex v∈G, then G is Hamiltonian.
• Theorem 5.7: given two nonadjacent vertices u and v in a graph G of order n such that deg(u)+deg(v)n, G+uv is Hamiltonian if and only if G is Hamiltonian. Note that G+uv denotes the graph G with a new edge between vertices u and v (which were formerly nonadjacent).
• Theorem 5.8: given a graph G with an order n≥3, if the relation 1≤j≤n/2 holds for every integer j and the number of vertices in G with a degree of at most j is less than j, then G is Hamiltonian.
• Theorem 5.9 Handshaking lemma for digraphs: given a digraph D with size m and V(D)={v₁,v₂,…,v_n}, the equation below holds.

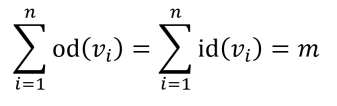
• Theorem 5.10: if a digraph D contains a u-v walk with a length of L, then D contains a u-v path with a length of at most L.
• Theorem 5.11: a digraph D is strong if and only if D contains a closed spanning walk.
• Theorem 5.12: a nontrivial connected digraph D is Eulerian if and only if od(v)=id(v) for each vertex v∈D.
• Theorem 5.13: a nontrivial connected graph G has a strong orientation if and only if G does not contain any bridges.
• Theorem 5.14: a tournament T is transitive if and only if T does not contain any cycles.
• Theorem 5.15: if u is a vertex with a maximum outdegree for a tournament T, then d(u,v)≤2 for every vertex v∈T.
• Theorem 5.16: every tournament T contains a Hamiltonian path.
• Theorem 5.17: every vertex in a tournament T which is nontrivial and strongly connected belongs to a directed 3-cycle.
• Theorem 5.18: a nontrivial tournament T is Hamiltonian if and only if T is strongly connected.
• Theorem 5.19: given a strongly connected tournament T with an order n≥4, there exists a vertex v such that T – v is also a strongly connected tournament.

Application: methods of proof

New mathematical concepts and tools are made through proofs. Using a series of logical steps, previously unrealized insights about the universe can be uncovered. Existing definitions and theorems are built upon, allowing an ever-expanding system of truth to develop, a system known as mathematics.

• Direct proof: a sequence of statements which starts with a given statement p and ends by proving a statement q. Each successive statement must logically follow from the previous statement.
• Proof by contradiction: by assuming that the negation of a statement q is true and then finding a logical contradiction, q can be proven. Negation is a logical operator denoted as ¬ If ¬q is true, then q is false. If ¬q is false, then q is true.
• Contrapositive proof: the statements p⇒q and ¬p⇒¬q are logically equivalent, so p⇒q can be proven by proving the contrapositive ¬p⇒¬q.
• Proving a biconditional: a logical biconditional is denoted as p⇔q, “p if and only if q,” p⇒q and q⇒p, or “p is necessary and sufficient for q.” Biconditionals can be proven in several ways. (i) By proving p⇒q and q⇒ (ii) By proving p⇒q and ¬p⇒¬q. (iii) By proving ¬q⇒¬p and q⇒p. (iv) By proving ¬q⇒¬p and ¬p⇒¬q.
• Proof by induction: consider a true basis statement p₁ that is true and an infinite sequence of statements p₁⇒p₂⇒p₃⇒…⇒p_n such that each statement logically implies the next in the sequence. If we know that p₁ is true, then all the other statements are also true. To prove by induction, show that p₁ is true and then show that p_n⇒p_n+1 for all n.
• Proof by cases: some proofs can be simplified by breaking the problem into cases and proving each case separately (i.e. proving a statement for even numbers and then for odd numbers).

Application: statistical properties of graphs

Graph theoretic models of complex networks can be analyzed using statistical properties. Such properties are useful for many real-world technological, social, and biological networks. In particular, network properties have revealed insights about the brain and may serve as a quantitative diagnosis method for mental illnesses, neurodegenerative diseases, and other disorders of the nervous system.

• Mean vertex degree: the average degree of vertices in a network.
• Degree distribution: the set of all vertex degrees in a network ordered in a sequential manner (often by increasing degree value). Depending on the particular network, this can result in Gaussian, bimodal, skewed, or other types of distribution.
• Assortativity: a measure of degree correlation between adjacent vertices, often described by an assortativity coefficient r, a Pearson correlation coefficient computed using the degrees of all adjacent vertex pairs in a network. In the formula below (for undirected networks), q_j represents the number of edges incident on a vertex j with the exception of the edge between vertex j and vertex k. Likewise, q_k represents the number of edges incident with a vertex k with the exception of the edge between vertex k and vertex j.

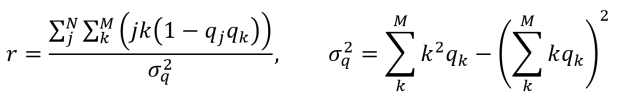
• Clustering coefficient: given a vertex v, its clustering coefficient C is defined as the number of edges s among the set of N vertices adjacent to v over the maximum possible number of edges among said vertices. Note that this measure excludes the edges incident with v itself.

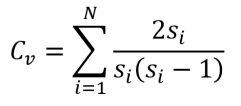
• Mean path length: the average number of vertices traversed by the paths in a network.
• Efficiency: the inverse of a path length L given by 1/L, often used because it is more convenient for certain topological analyses of networks.
• Connection density: given a network of order n, its connection density d (also called cost) is defined as the network’s size S over the size of a complete graph of order n.

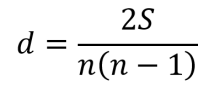
• Closeness centrality: a measure of how many shortest paths between all pairs of vertices in a network pass through a given vertex u. The higher the closeness centrality, the closer u is to all other vertices in the network. In the equation below, N is the network’s order and v represents all of the vertices such that v≠u.

• Robustness: describes how much a network’s overall structure and statistical properties are altered upon perturbations like vertex deletions, edge deletions, vertex insertions, edge insertions, reversals of edge directionalities, and changes to edge weight. Robustness can be quantified by a diverse array of methods.
• Modularity: a term describing networks which include densely interconnected subgraphs known as modules. Not many edges are formed between vertices within a given module and vertices outside of said module. Modularity can be quantified by a diverse array of methods.
• Hubs: vertices with high closeness centrality values are called hubs. Alternatively, vertices with high degree can be called hubs.
• Provincial hubs: vertices found inside of modules are often called provincial hubs.
• Connector hubs: vertices which link distinct modules are often called connector hubs.
• Small-worldness: a property proportional to a network’s mean clustering coefficient over its mean path length. Networks with high small-worldness are called small-world networks.

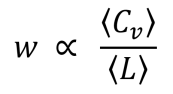
• Scale-free: a network with a degree distribution that is described by a power law is a called scale-free. Power law distributions are defined by the probability mass function P(X=k)=k^-λ where k is the degree of a given vertex in the network and λ is a constant parameter specific to the network under investigation.

Application: the graph Laplacian and random walks

The graph Laplacian (also called the Laplacian matrix) allows a variety of useful analyses to be carried out on graphs. In particular, it can probabilistically describe a random walker’s activities. Random walkers can be thought of as objects which stochastically “jump from vertex to vertex” on a graph.

• Degree matrix: a matrix D with the degrees of a graph G along the diagonal. The remaining entries of D are zeros. For digraphs, the degree matrix may describe either the indegree or the outdegree.
• Laplacian matrix: given a degree matrix D and an adjacency matrix A which describe some graph, the graph’s Laplacian matrix or graph Laplacian is L=D–A.
• Random walk normalized Laplacian: a matrix defined by L^rw=D^-1 The random walk normalized Laplacian can also be computed by L^rw=I_n–D^-1A where I_n is the identity matrix.
• Transition matrix for a random walker: the term D^-1A from the random walk normalized Laplacian represents the transition matrix P for a random walker on a graph G. For a vertex i∈G and the i^th standard basis vector e_i, the vector x=e_iP is a probability vector describing the distribution of a random walker’s possible locations after taking a single step from vertex i. (Note that a probability vector is a vector of values which sum to one and represent probabilities). If q₀ is a probability vector describing the initial distribution of a random walker’s possible locations and q_t is a probability vector describing the distribution of the random walker’s possible locations after t steps, then q_t=q₀P^t.

References

1. Chartrand G, Zhang P. 2013. A First Course in Graph Theory. Dover Publications.
2. Bullmore E, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186.

     Humans have puzzled over the possibility of an objective moral theory since the dawn of philosophical inquiry. Many argue that morality is socially constructed rather than based in physical laws. Ethical relativists like Foucault (Wilkin, 1999) and sophists like Protagoras (Guthrie, 1969) have proposed that fundamental ethical truths do not exist. Along a similar line of reasoning, Richard Joyce contends that biases imposed by human evolutionary psychology invalidate the concept of fundamental morality since all ethical ideas depend on our evolutionary history (Joyce, 2001). But certain nondualist approaches to cognitive philosophy may provide a new perspective on this notion, a perspective in which ethical truths are both fundamental and relative. I propose that, if consciousness and emotion derive directly from physical processes, then objective morality exists, but continuously varies over space and time.

     For my theory of objective morality, I assume the panpsychist idea that conscious experience is a property of matter, analogous to mass or charge (Seager, 1995). According to this view, specific physical patterns may give rise to specific emotional states in a one-to-one correspondence, making qualia omnipresent. It should be noted that if panpsychism is true, the stochastic flickers of qualia associated with most matter would likely feel primitive enough that they would be unrecognizable by human standards. Next, I apply an authenticity-driven form of existentialism to this panpsychist perspective, allowing physically-encoded emotions to take on intrinsic meaning. In this writing, I exclude “meaninglessness” from existentialism and instead focus on the aspects of existentialism which involve people creating meaning for themselves (Holt, 2012). The distribution of emotional states across the universe may serve as a starting point for a physical description of ethics. By combining panpsychism with physicalism and existentialism, morality can be linked to physics in an objective fashion.

     Despite its past association with metaphysics, panpsychism is rekindling among contemporary thinkers as an explanation for consciousness (Strawson, 2006). Integrated information theory or IIT (Oizumi, Albantakis, & Tononi, 2014) is a mathematical formulation which seeks to quantify consciousness using the information arising from dynamical systems. Galen Strawson has argued that IIT implies panpsychism since all physical structures contain some amount of information (Strawson, 2006). Furthermore, Adam Barrett has proposed modifications to IIT which may help account for fundamental physical interpretations of the universe like quantum field theory (Barrett, 2014). Panpsychic descriptions of reality are reentering philosophical and scientific discourse as new data are acquired and new theoretical interpretations develop.

     But many still find the concept that inanimate objects may possess primitive qualia to be absurd. To counter this presumption, consider a fragment of quartz resting on a ridge. As the sun rises, photons excite the atoms on the crystal’s surface, causing thermal oscillations to propagate into the quartz. This thermal diffusion is modulated by crystallographic defects, causing a heterogeneous distribution of heat inside the rock. As dusk falls, the quartz fragment begins to cool, emitting heat at varying rates across the surface. The particular rates are influenced directly by this quartz specimen’s pattern of internal defects. Next, consider a mouse, also located on the ridge. As the sun rises, photons excite the retinaldehyde molecules in the mouse’s eyes, triggering signal transduction via electrochemical systems. This signal moves into the mouse’s brain, where it propagates through a series of neural pathways, causing a heterogeneous distribution of neural activity. Soon, the signal’s interaction with preexisting brain structures is translated into a motor action; the mouse blinks and looks away from the bright illumination. The particular motor response is modulated by the structural organization of this mouse’s brain at the given time. The quartz and the mouse both receive sensory inputs, process them according to internal properties, and then give motor outputs. Although the rock’s “brain” is much more disorganized and chaotic than the mouse’s brain, it operates by the same basic principles and could plausibly experience a primitive form of consciousness. As such, the possibility of panpsychism cannot be readily dismissed as absurd or metaphysical.

     Another prominent objection to panpyschism arises from brain processes which occur in a subconscious fashion. For instance, activity in the primary visual cortex (V1) does not correlate with conscious visual experience except for a few special cases (Crick & Koch, 1995) (Boyer, Harrison, & Ro, 2005) (Boehler, Schoenfeld, Heinze, & Hopf, 2008). However, the presence of subconscious neural events does not necessarily indicate that the said events are subconscious from the viewpoint of their associated anatomies. Instead, anatomical structures like V1 may experience their own independent qualia. The full informational content of their perceptions may not be transmitted or translated into the brain areas like the prefrontal cortex (PFC) which can be identified with a patient’s sense of self (Mitchell, Banaji, & Macrae, 2005). Of course, some data does transfer into higher brain regions to facilitate processes like vision, but the information undergoes an extensive series of transformations before arriving at the PFC and other regions associated with conscious processing. For this reason, the “unconscious anatomies” objection is insufficient to invalidate panpsychism.

     While existentialism is often linked to both authenticity in developing a personal outlook on life and to a sense of nihilistic meaningless, I use a modified interpretation of existentialism within this essay. I discard the nihilistic component of existentialism and enhance its emotional authenticity to operate in a manner analogous to Cartesian view around the ontology of thought, cogito ergo sum (Murdoch, Cottingham, Descartes, & Stoothoff, 1985). My interpretation of existentialism revolves around idea that emotions possess intrinsic validity in the same way Descartes argued for the intrinsic validity of consciousness. By applying this form of existentialism to physicalist panpsychism, an objective theory of morality gains feasibility.

     My proposed ethical theory does not mean that morality is uniform throughout the cosmos. Equipping the distribution of emotional states or “affective manifold” with existentialism allows for objective morality to continuously vary as informatic patterns change over space and time. Manifolds are mathematical objects which can be informally described as deformed versions of spaces such as the real line, plane, or three-dimensional Euclidean space. Although the affective manifold would not generally exhibit universal emotional uniformity, particular conformations of the manifold may still represent ultimate maxima or minima over all reality. An ultimate maximum may resemble the Buddhist concept of Nirvana, while an ultimate minimum may resemble a hell far worse than any imagined by the world’s religions. These extrema describe states of absolute moral “good” and absolute moral “bad” in a fashion which is fundamentally linked to physics. While this theory connects morality to fundamental processes in the universe, the said morality is also dependent on spatiotemporal coordinates. Ethical truths vary over the affective manifold except when the manifold holds a constant value across the entire cosmos as in the Nirvana and hell cases. In this way, morality may simultaneously take on objective and relative characteristics. Natural law exists, but a given natural law rarely takes on the same form across any two distinct subsets of spacetime.

     As an example, consider a subset of spacetime which includes only a human named Zebadiah during a specified eight-second time interval. Zebadiah feels unjustly underpaid at his job. During the eight-second period, he notices a fifty-dollar bill sitting on the desk of his boss, Enrique. He is alone and could easily snatch the money without consequences. Zebadiah pockets the fifty-dollar bill and does not experience guilt. He feels that this action is morally correct. Inside the spatial bounds of Zebadiah’s brain and the temporal bounds of the eight-second interval, this action is indeed morally correct on a fundamental level. But after the eight seconds have passed, Zebadiah recalls that Enrique’s wife is ill and cannot work, so Enrique is struggling financially. Zebadiah feels a rush of guilt and places the money back on Enrique’s desk. In this new time period, the Zebadiah-specific natural law has changed. Unknown to Zebadiah, Enrique was watching the entire time via a newly-installed security camera. During both time intervals, Enrique feels that Zebadiah is only taking a moral action if he does not steal the money. From an existential viewpoint, all the described perspectives are valid. Panpsychism connects this existentialism to physical processes, supporting moral objectivity on given subsets of the affective manifold.

     Morality is objective, but not absolute except for the specific situations in which the affective manifold is configured in a universally desirable or undesirable manner. Using a physics-based form of panpsychism along with an interpretation of existentialism which grants intrinsic validity to a subject’s emotions, the affective manifold emerges as a possible source of objective ethics. In most distributions of emotional states over the cosmos, ethical truths undergo continuous variation as spatial and temporal coordinates change. In this way, morality can be quite different for distinct persons and even for individual persons at different times. However, it remains an absolute ethical truth that reconfiguring the affective manifold such that all matter in the universe is optimized for generating a supremely positive emotional state represents a morally ideal action. Likewise, reconfiguring the affective manifold to generate a supremely negative emotional state represents an absolute moral wrong. My objective theory of morality may provide a new perspective on the study of ethics and so help to more effectively derive insights around contemporary ethical problems.

References

Barrett, A. (2014). An integration of integrated information theory with fundamental physics. Frontiers in Psychology. Retrieved from https://www.frontiersin.org/article/10.3389/fpsyg.2014.00063

Boehler, C. N., Schoenfeld, M. A., Heinze, H.-J., & Hopf, J.-M. (2008). Rapid recurrent processing gates awareness in primary visual cortex. Proceedings of the National Academy of Sciences, 105(25), 8742 LP-8747. Retrieved from http://www.pnas.org/content/105/25/8742.abstract

Boyer, J. L., Harrison, S., & Ro, T. (2005). Unconscious processing of orientation and color without primary visual cortex. Proceedings of the National Academy of Sciences of the United States of America, 102(46), 16875 LP-16879. Retrieved from http://www.pnas.org/content/102/46/16875.abstract

Crick, F., & Koch, C. (1995). Are we aware of neural activity in primary visual cortex? Nature, 375(6527), 121–123.

Guthrie, W. K. C. (1969). The Sophists. Cambridge University Press.

Holt, K. (2012). Authentic Journalism? A Critical Discussion about Existential Authenticity in Journalism Ethics. Journal of Mass Media Ethics, 27(1), 2–14. http://doi.org/10.1080/08900523.2012.636244

Joyce, R. (2001). The Myth of Morality. Cambridge University Press.

Mitchell, J. P., Banaji, M. R., & Macrae, C. N. (2005). The Link between Social Cognition and Self-referential Thought in the Medial Prefrontal Cortex. Journal of Cognitive Neuroscience, 17(8), 1306–1315. http://doi.org/10.1162/0898929055002418

Murdoch, D., Cottingham, J., Descartes, R., & Stoothoff, R. (Eds.). (1985). Principles of Philosophy. In The Philosophical Writings of Descartes (Vol. 1, pp. 177–292). Cambridge: Cambridge University Press. http://doi.org/DOI: 10.1017/CBO9780511805042.007

Oizumi, M., Albantakis, L., & Tononi, G. (2014). From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLOS Computational Biology, 10(5), e1003588. Retrieved from https://doi.org/10.1371/journal.pcbi.1003588

Seager, W. E. (1995). Consciousness, information, and panpsychism. Journal of Consciousness Studies, 2(3).

Strawson, G. (2006). Realistic monism: why physicalism entails panpsychism.

Wilkin, P. (1999). Chomsky and Foucault on Human Nature and Politics: An Essential Difference? Social Theory and Practice, 25(2), 177–210. Retrieved from http://www.jstor.org/stable/23559137

     Neuroecologies, cybernetic systems which combine biological and technological components, may streamline human interactions with their environment and counteract issues like pollution and climate change. Today, humans occupy too many ecological niches for long-term sustainability. If we continue to outcompete other species, we will observe deadly systemic bifurcations that lead to desertification, coastal submergence, and even more widespread extinctions. However, the interdependence of existing socioeconomic structures makes them difficult to uproot in order to avert catastrophe. To overcome this challenge, I propose that humans must integrate into their environments without sacrificing existing structures, instead metamorphosing those structures into more sustainable forms through improved technologies. In particular, the worlds of electronics, nanoscience, and synthetic biology must merge into the meadows, forests, and oceans. As written by Richard Brautigan in his 1967 poem, All Watched Over by Machines of Loving Grace, the “mammals and computers [will] live together in mutually programming harmony.”

     Traditionally, environmentalist viewpoints have divorced technology and nature, framing human influence as corrupting and impure. However, this represents an incorrect and ultimately counterproductive approach. Humans and their creations are no more separate from nature than termites and their mounds, beavers and their dams, or bacteria and their metabolic byproducts. While human impact on the environment has occurred at a rapid pace, this does not mean that humans are inherently less ethical than other organisms. Framing the technological humans as evil is a mistake since this ideology “drives underground” many possible solutions to environmental challenges.

     Many naturalists have supported anti-interference arguments with the fact that some technology has contributed to environmental damages. However, framing any particular technology as representative of all technology is misguided in an analogous way to cultural prejudice. Few would advocate judging the entire population of China based on an interaction with a single Chinese person. Likewise, it should be clear that the technologies which have contributed to climate change should not represent the philosophical concept of technology as a whole.

     Unlike most other organisms, humans possess a potent ability to simulate possible future scenarios. This ability arises from internal biological cognition, social exchange of knowledge, and technological augmentations. On its own, the human brain can generate plans for behavior many years into the future. In societies, networks of human brains act as a form of distributed superintelligence, agglomerating and refining individual predictions (Lenartowicz, 2017). The outsourcing of cognitive tasks to computers, pencils, and other technologies provides an immense expansion to the human noosphere. This combined global cortex has the power to analyze, predict, and act to tackle today’s greatest challenges.

     Biological and technological systems often share characteristics. From a network perspective, both usually possess a small-world structure (Sporns, 2009) (Newman, 2003). Small-world networks (supplementary Fig. S1C-D) have small mean path lengths and high clustering. For reference, mean path length is the average number of jumps taken to traverse between any pair of nodes in a network and clustering measures the connectivity among a given node’s nearest-neighbors (supplementary Fig. S1A-B). In addition, both biological and technological networks tend to exhibit resilience against random removal of nodes and vulnerability to targeted removal of highly interconnected nodes (Newman, 2003). Such network properties show remarkable universality across technology and biology.

     From a control theory perspective, biological and technological systems share modules and protocols (Csete, 2002). Modules are subsystems that utilize interfaces to other modules and work with some degree of independence. Biological modules can be seen in macromolecular complexes, membrane-bound compartments, cells, oscillating neural circuits, organs, as well as in ecosocial structures like packs of wolves and coral reefs. Technological modules arise in circuit components like flip-flops, in microprocessors, in network-connected computational devices, stations on assembly lines, and in components of infrastructure like hospitals and schools.

     Protocols are rules which manage the flow of ordered operations within systems (Csete, 2002). Biological protocols arise from information encoded in nucleic acids, epigenetic regulatory networks, neural ensembles, and ecological competition structures. Within such biological and technological protocols, feedback loops are universal. Feedback facilitates stable oscillations, system-scale or subsystem-scale adaptation to external stimuli, and discourse among modules.

     Since biology and technology operate by common principles, the engineering techniques applied in technological systems can be adapted to engineering biological systems and engineering interfaces between systems. Of course, doing this will also require recognizing differences and working to optimize the characteristics of all the systems involved in order to more seamlessly merge our technology and environment.

     For illustrative purposes, I will briefly outline a potential urban implementation of neuroecologies, a fictional city called Las Futuras. The skyscrapers of Las Futuras are wrapped in a silky, biocompatible polymer (Fig. 1B). Embedded in the polymeric matrix are nanomachines which recycle chemical waste products into nutrients, antioxidants, water, and molecules that chelate toxins and facilitate their traffic to more intensive treatment nodules. Cybernetic fireflies and bioluminescent trees illuminate the metropolis at night. There are no roads, the ground is overgrown with sensory flowers that monitor conditions and transmit data through conductive root networks, glistening metabolic blobs which assemble swarms of nanorobotic gardeners on command (Fig. 1C), and gossamer membranes for collecting solar energy.

     Enhanced herbivores and insects wander freely, instinctively consuming the fruitlike globules growing out of the buildings. There is no predation as all predators have either been transformed into herbivores or their populations have been phased out by reproductive methods. Because of this and the fact that the animals may live for hundreds or even thousands of years, their fertility rates are modulated by AI savants who continuously oversee the organismic network and prevent catastrophic bifurcations from triggering issues like overpopulation and starvation.

     The reason that few humanoid creatures are visible is that they exist elsewhere. Inside the skyscrapers, dense cores of computronium (Fig. 1A) simulate vast and beautiful worlds, kaleidoscopic utopias in which humanity’s billions and their AGI children may reside without overconsumption of resources. These people do have the option of entering android bodies and exploring realspace, but this exploration usually involves visiting locations other than Earth. As such, the neuroecologies remain sparsely populated by androids and their resource demands are minimal.

Figure 1 (A) Top view of the speculative urban neuroecology dubbed Las Futuras. Some skyscrapers (hexagonal structures) contain computronium for simulating uploaded minds and their virtual worlds, others manufacture materials and machines as needed by the system, still others recycle waste products. (B) Mesoscale view of a region within Las Futuras. Engineered trees exhibit bioluminescence. Nanomachines which recycle atmospheric pollutants are found in the walls of the skyscrapers. (C) Ground-level view of a region within Las Futuras. Fruitlike globules provide nutrients for cybernetic wildlife, including modified microorganisms and nanorobots. Solar membranes gather energy for local use, though more extensive solar farms exist outside the metropolitan area. Wriggling wormlike creatures tend to various macroscale tasks. Sensory flowers (not shown) monitor ambient conditions and route information into the conductive root network. This extensive system of roots provides a method of rapidly transporting data into the noosphere. Most organisms and devices are compatible with the roots and can easily link their nervous systems to the network.

     Although this kind of world might seem distant, there is a real possibility that it will be achievable before the end of the 21^st century. As a result of exponential trends in computer science and bioinformatics, many futurists argue that we are approaching a technological singularity. If this event occurs, it will be marked by an intelligence explosion which radically transforms life on Earth and beyond. The technological singularity may come from artificial superintelligence, self-aware computer networks, biological enhancement, or from the merging of humans and machines (Vinge, 1993). National Medal of Technology recipient Ray Kurzweil proposes that the technological singularity may occur as early as 2045, providing cognitive abilities up to a billion-fold more powerful than the entirety of today’s human race combined (122). This prediction may initially sound outrageous, but Kurzweil has shown a remarkable ability to accurately envision future events as evidenced by his numerous successful predictions; for instance, former world chess champion Garry Kasparov losing his games against IBM’s Deep Blue chess computer in 1997. If the singularity comes to pass, it will provide the intellectual and robotic resources necessary to merge technology and the environment.

     For some, my vision of the future might initially sound unsettling as it is a very different world than the world to which we are accustomed. But throughout evolutionary history, the ecological scene has continuously metamorphosed. In the Precambrian, aquatic metazoans (multicellular organisms) were only just beginning to emerge and the land was populated only by cyanobacterial mats (Horodyski and Knauth, 1994). Today, a rich and beautiful biosphere thrives across the air, land, and sea. The prospect of transformation need not be frightening. Technology is a part of nature, facilitating the metamorphosis. We have the ability to carry out this transformation, guiding unstable human and nonhuman ecologies into unified, sustainable neuroecologies.

References

Brautigan. “All Watched Over by Machines of Loving Grace.” All Watched Over by Machines of Loving Grace, Communication Company, 1967.

Bullmore, Ed, and Olaf Sporns. “Complex brain networks: graph theoretical analysis of structural and functional systems.” Nature Reviews Neuroscience, vol. 10, no. 3, Apr. 2009, 186–198., doi:10.1038/nrn2575.

Csete, M. E. “Reverse Engineering of Biological Complexity.” Science, vol. 295, no. 5560, Jan. 2002, pp. 1664–1669., doi:10.1126/science.1069981.

Horodyski, R. J., and L. P. Knauth. “Life on Land in the Precambrian.” Science, vol. 263, no. 5146, 1994, pp. 494–498., doi:10.1126/science.263.5146.494.

Kurzweil, R. (2005). The Singularity is Near: When Humans Transcend Biology. New York: Viking.

Lenartowicz, Marta. “Creatures of the semiosphere: A problematic third party in the ‘humans plus technology’ cognitive architecture of the future global superintelligence.” Technological Forecasting and Social Change, vol. 114, 2017, pp. 35–42., doi:10.1016/j.techfore.2016.07.006.

Newman, Mark. “The Structure and Function of Complex Networks.” SIAM Review, vol. 45, no. 2, Mar. 2003, pp. 167–256., doi:10.1137/S003614450342480.

Vinge, Vernor. “The Coming Technological Singularity: How to Survive in the Post-human Era.” Interdisciplinary Science and Engineering in the Era of Cyberspace, Dec. 1993.

 

Supplementary Figure S1 (A) The clustering coefficient for a node is the number of links among its nearest neighbors divided by the maximum number of links among those neighbors. (B) The path length between two nodes is the minimum number of edges which must be traversed in order to reach one node from the other. (C) Small-world networks are extremely common in biological and technological systems. Here, a randomly generated small-world network is depicted. (D) Small-worldness is proportional to the mean clustering coefficient over the mean path length. Note that the N^-1 terms cancel since they are the same in the numerator and the denominator for a given network with N nodes.

 

Nanowire arrays restore vision in blind mice

• Nanowire arrays were developed and implanted in the retinas of blind mice to replace photoreceptor cells (A).
• The nanowires consisted of titanium dioxide wires decorated with gold nanoparticles.
  • TiO₂ nanowires are known to generate photocurrents upon exposure to UV light.
  • Decorating the wires with gold nanoparticles enhances this effect and allows for blue and green visible light to also trigger photocurrents.
  • The photocurrents for blue and green light were much lower than the photocurrents for near-UV light, but still high enough to be useful.
• Patch-clamp recording was used to measure the responses of retinal ganglion cells (RGCs) in controls and in mice equipped with nanowires to near-UV, blue, and green light.
  • The RGCs in wild-type mice were responsive to near-UV, blue, and green light.
  • RGCs with nanowires were responsive to near-UV light (B).
  • RGCs with nanowires were responsive to blue and green light (C), though the latencies were longer compared to near-UV case, likely because of their smaller photocurrents.
• The responses of nanowire-equipped RGCs to varying light spot diameters were also tested (D).
  • For near-UV light, RGCs could be reliably activated with spots of about 50-100 µm (and larger spots).
  • For blue and green light, RGCs could be reliably activated with spots of about 200-300 µm (and larger spots).
• Pupillary reflex improvements in the nanowire-carrying mice supported the conclusion that the nanowire implants had partially restored vision.

Reference: Tang, J., Qin, N., Chong, Y., Diao, Y., Y., Wang, Z., … Zheng, G. (2018). Nanowire arrays restore vision in blind mice. Nature Communications, 9(1). doi:10.1038/s41467-018-03212-0

 

Surface chemistry governs cellular tropism of nanoparticles in the brain

• The interactions of polylactic acid (PLA) nanoparticles with the brain microenvironment were studied. It should be noted that this paper also investigated PLA nanoparticle interactions with glioblastoma tumors, but that topic will not be discussed in this summary.
• PLA nanoparticles were infused into rat brains. Four types of PLA nanoparticle formulation were tested, each bearing a different functional group.
  • PLA nanoparticles coated with polyethylene glycol (PEG), hyperbranched glycerol (HPG), HPG-CHO (aldehydes instead of vicinal diols), and unmodified PLA nanoparticles were examined.
  • PLA-PEG and PLA-HPG nanoparticles have decreased immunogenicity. PLA-HPG-CHO nanoparticles are less immunogenic as well as exhibiting bioadhesivity.
  • The nanoparticles were engineered to be brain-penetrating. They possessed neutral or negative surface charge, diameters of under 100 nm, hydrodynamic diameters (a measure which incorporates the movement of polymer chains in the nanoparticles) of under 150 nm, and did not aggregate in cerebrospinal fluid. In addition, they were fluorescently labeled with the chemical dye DiA.
  • All nanoparticle formulations diffused over volumes of about 40 mm³. The diffusion volumes were also fairly homogenous, though some minor variation occurred (A).
• Interactions with neurons, astrocytes, and microglia were tested. Nanoparticles were infused into the brain and allowed to diffuse. Relative abundances of nanoparticles in the three cell types were analyzed using fluorescence-activated cell sorting to measure mean florescence intensity (MFI) within individual cells (B).
  • PLA-PEG and PLA-HGP nanoparticle uptake was distributed fairly evenly among the cell types. They also exhibited lower total uptake than PLA-HPG-CHO nanoparticles.
  • In addition to showing higher total uptake, PLA-HPG-CHO nanoparticles exhibited preferential uptake by microglial cells and decreased uptake by neurons.
• Confocal fluorescence microscopy was used to image tissue samples with infused nanoparticles.
  • Neuron morphology was not significantly affected by any of the nanoparticle types.
  • PLA, PLA-PEG, and PLA-HPG-CHO (but not PLA-HPG) nanoparticles caused astrocytes to display upregulated GFAP protein, indicating some level of immunogenicity (C).
  • PLA and PLA-HPG-CHO nanoparticles caused amoeboid morphology in microglia, indicating that they had entered an immunologically active state. PLA-PEG and PLA-HGP nanoparticles allowed microglia to stay in a ramified (branched) state, indicating lack of immunological response (D).
  • In the displayed confocal microscopy images (taken after 4 hours of diffusion), nanoparticles are stained red, nuclei blue, and GFAP white.

Reference: Song, E., Gaudin, A., King, A. R., Seo, Y., Suh, H., Deng, Y., … Saltzman, W. M. (2017). Surface chemistry governs cellular tropism of nanoparticles in the brain. Nature Communications, 8, 15322. doi:10.1038/ncomms15322

Andromeda Spaceways Magazine #70 can be accessed at the link below. Visit pages 89-90 to read my poem, The Sonata Machine.

ASM70