Manifolds

• Although differential geometry usually involves smooth manifolds, topological manifolds provide the foundation for understanding smooth manifolds.
• Topological manifolds are a type of topological space which must satisfy the conditions of Hausdorffness, second-countability, and paracompactness (see Notes on Topology).
• In addition, topological manifolds must be locally homeomorphic to Euclidean space, ℝⁿ.
• In order to be locally homeomorphic to Euclidean space, the formalisms below must hold.

• This means that, for every point x in a locally Euclidean topological space X, there exists an open set U such that x belongs to U and there exists a homeomorphism h from ℝⁿ to U (and its inverse). These homeomorphisms are called charts. The combination of charts which covers X is called an atlas.
• For an atlas, two charts can overlap on a manifold. The intersection of these two charts is an open set which maps to the same region of Euclidean space. Transition maps are composition functions f(g^-1) = f∘g^-1 and g(f^-1) = g∘f^-1 which map the open sets in ℝ²to the manifold (by the inverse function) and then map back to Euclidean space (by the function which describes the other homeomorphism). This is also called a coordinate transformation.

• If a manifold’s transition maps are all at least once differentiable (C¹), then the manifold is called a differentiable manifold. If the transition maps are all infinitely differentiable (C^∞), then the manifold is called a smooth manifold.

Dot products on smooth manifolds

• The metric tensor allows generalization of the dot product for vectors on manifolds and is given by the equation below. Here, u and v are input vectors. The superscript and subscript indicate that uⁱ is represented as a column vector and v_j is represented as a row vector (covector to uⁱ) inside the summation. The matrix g_ij is a coefficient matrix which modifies the initial coordinate system for a given manifold. The summation is over matrix indices i and j where i=j.

• To see how this equation works, consider using metric tensor to describe the dot product of two vectors in ℝ². In this case, g_ij is simply the 2×2 identity matrix.

• For manifolds in general, the coefficient matrix g_ij is usually not the identity matrix. Instead, the entries of g_ij are given by the equation below involving the Jacobian matrix J.

• To use this equation, new coordinates must be defined in terms of Euclidean coordinates. In order to understand this, consider the example of polar coordinates. The polar coordinate formulas are operated on by the Jacobian. When inputted into the formula for the coefficient matrix, they simplify to the result below.

• Any set of alternative coordinates written in terms of Euclidean coordinates can be used to generate a g_ij matrix by this process.
• An interesting application of the metric tensor is to compute the generalized dot product of two vectors on a surface (2-manifold). The vectors “start out” in ℝ², but then are mapped onto the surface, which is embedded in ℝ³. To accomplish this, the ℝ² coordinates are represented in ℝ³ by using zero for the z-components. Note that the plane is assumed to be perpendicular to the surface in this scenario.

• Given a pair of vectors u and v tangent to a point on a parametric surface (2-manifold), the lengths of the vectors and the angle between them can be computed using the metric tensor. The lengths are given in the top equations and the angle is given in the bottom equations (below).

Arc lengths on smooth manifolds

• The metric tensor can be used to determine the distance between the points γ(t₁) and γ(t₂) on a manifold. The vector-valued function γ(t) defines a parametric curve on the manifold. Here, g_ij is generated using the Jacobian of the parametric functions in γ(t). The components γⁱ and γ^j are equivalent when i=j since they represent the same components. The absolute value is included to keep the term under the square root positive.

• Consider the example of a parametric curve in ℝ² which is mapped onto a 2-manifold embedded in ℝ³. Here, the arc length of such a curve is computed.

Integration on smooth manifolds

• Integration can be performed on surfaces (2-manifolds) using surface integrals. Furthermore, this method can be generalized to volumes and hypervolumes on n-dimensional smooth manifolds.
• The surface integral of a region on a 2-manifold embedded in ℝ³ can be computed by the equation below. The double-struck bars indicate magnitude. Here, the surface is given as a function z(x,y).

• It should be noted that r may represent any parameterized parametrized surface (not just a surface given as z(x,y)). The more general case of a surface embedded in ℝ³ is given below.

• Using some algebraic manipulations, the surface integral can be rewritten as the equation below. The matrix g represents the metric tensor (generated by applying the Jacobian to the parameterized function r).

• In this form, the surface integral can easily be generalized to higher dimensions so as to integrate volumes and hypervolumes on smooth manifolds. Below, a volume integral on a smooth 3-manifold is given.

• For integrating a hypervolume on an n-dimensional smooth manifold, a generalized version of the surface and volume integrals can be used.

by Logan Thrasher Collins

Overview of Drosophilia’s Eyes and Visual Pathway

• Insect eyes are composed of repetitive units called facets.
• The eyes found in most insects can be categorized as apposition eyes or superposition eyes. In apposition eyes, the photoreceptors are isolated from each other within facets. In superposition eyes, which are often found in nocturnal insects, many facets act together without partitioning the photoreceptors. Here, apposition eyes will be focused upon.
• In the eyes of dipterans (flies), there are six photoreceptors (R1-R6) surrounding a stacked pair of central photoreceptors (R7-R8) within each ommatidium. Because of this arrangement, there are distinct axes along which light enters the photoreceptors in a single ommatidium.
• However, the photoreceptors in neighboring ommatidia take in light along parallel axes. The photoreceptors which receive light on parallel axes project to the same postsynaptic target.

• This kind of structure indicates that, unlike in some cartoons, insects do not see the world as “honeycomb pixels.” They form a unified neural representation of the environment. However, small dipterans like Drosophila (with fewer facets than larger insects like dragonflies) do have poor spatial resolution.
• Insect nervous systems generally include a head ganglion (brain), three thoracic ganglia, and several abdominal ganglia. However, Drosophila’s thoracic and abdominal ganglia are fused into a single thoracic ganglion.
• Drosophila’s thoracic ganglion is linked to the head ganglion via the cervical connective, a structure which contains about 3600 afferent and efferent axons.
• Drosophila’s head ganglion has a cortex composed of cell bodies which project inwards to form a structure called the neuropile. The neuropile consists of numerous fibers which synapse upon each other. (This kind of anatomical organization is common among all insects).
• The head ganglion in Drosophila is subdivided into the central brain, the subesophageal ganglion, and the primary sensory centers. The visual ganglia are among the primary sensory centers.

Visual Neuroanatomy in Drosophila

• Drosophila’s visual system is divided into three subcortical layers including the lamina, medulla, and the lobula and lobula plate. These structures form retinotopic maps and have repetitive columns.

• There is an optic chiasm (crossing of pathways from the two visual fields) from the lamina to the medulla and an optic chiasm from the medulla to the lobula complex.
• The central photoreceptors (R7-R8) project through the lamina and make synapses in the medulla. By contrast photoreceptors R1-R6 terminate in the lamina.
• The lamina column is called the cartridge. It contains lamina monopolar cells L1-L5, the centrifugal cells C1-C2, and the single T1 cell. All of these connect the lamina to different layers of the medulla. L1-L3 are postsynaptic to photoreceptors R1-R6.
• Every medulla column contains about sixty neurons. These neurons can be classified according to their anatomical connectivity.
  • The intrinsic medulla (Mi) neurons terminate within two or more layers of the medulla and do not send projections elsewhere.
  • Transmedulla ™ cells and bushy T2-T3 cells connect one or more layers in the medulla to the lobula.
  • Transmedulla Y-cells connect several layers within the the medulla to the lobula. Their axons bifurcate and project into both the lobula and the lobula plate simultaneously.
  • Bushy T4 cells connect the innermost layer of the medulla only to the lobula plate. The bushy T4 cells are called T4a-d depending on which layer of the lobula plate they terminate within.
  • The lobula and lobula plate are connected by bushy T5 cells. Some of the bushy T5 cells project into the most posterior layer of the lobula. The rest project into one of four layers in the lobula plate (and are called T5a-d depending on the layer).
  • In addition to columnar cells, there are many laterally oriented neurons in the medulla which form thin sheets perpendicular to the columns.
• Lobula plate tangential cells are a type of large neuron found in the lobula plate. The dendritic arbors of these cells are extensive enough that they can take inputs from thousands of different columns.

Drosophila Phototransduction

• Vertebrate photoreceptors hyperpolarize upon exposure to light and are active in dark conditions.
• By contrast, insect photoreceptors are depolarized under illumination.
• In addition, insect photoreceptors have more than three-fold higher temporal resolution than those found in vertebrates.
• Insect photoreceptors are densely packed along folded membranes which resemble microvilli. These membranes are called rhabdomeres.
• The rapid temporal response to light arises in large part from the high surface area of the rhabdomeres and the small distances required for signaling molecules to diffuse among the folds of membrane.

• Drosophila and vertebrates both transduce light using rhodopsin proteins with bound cofactors. While vertebrates carry the cofactor retinal, Drosophila instead uses a cofactor called 3-hydroxyl retinal. When exposed to a photon, this cofactor undergoes a cis-trans isomerization and the rhodopsin protein undergoes a conformational change to metarhodopsin.
• Insect meta-rhodopsin is stable and can easily convert back to rhodopsin without exchanging the cofactor molecule (unlike in vertebrates, which use a multistep process to exchange trans-retinal for cis-retinal and reset to rhodopsin).
• For Drosophila, phototransduction begins with the absorption of a photon by rhodopsin, which then converts into metarhodopsin. The metarhodopsin activates a G-protein. The G_α subunit then activates phospholipase C (PLC) which cleaves the phospholipid PIP₂ into IP₃ and diacylglycerol. These second messengers lead to the opening of calcium channels (which are called trp and trp-like). The resulting influx of calcium depolarizes the photoreceptors and triggers release of the neurotransmitter histamine (which is inhibitory in this context). Finally, calcium is rapidly removed by an antiporter protein called Sodium-Calcium exchanger (CalX).

References

Borst, A. (2009). Drosophila’s View on Insect Vision. Current Biology, 19(1). doi:10.1016/j.cub.2008.11.001

Montell, C. (2012). Drosophila visual transduction. Trends in Neurosciences, 35(6), 356-363. doi:10.1016/j.tins.2012.03.004

This material was originally published in DUJS 17S.

The Potential of Brain Emulation

The human brain has been described as “the most complex object in the universe.” Its network of 86 billion neurons,¹ 84 billion glial cells, and over 150 trillion synapses² may seem intractable. Nonetheless, efforts to comprehensively map, understand, and even computationally reproduce this structure are underway. The Human Brain Project (HBP) and its precursor, the Blue Brain Project, have spearheaded the brain simulation goal,³ along with two other notable organizations – the China Brain Project and the BRAIN Initiative.

Whole brain emulation (WBE), the computational simulation of the human brain with synaptic (or higher) resolution, would fundamentally change medicine, artificial intelligence, and neurotechnology. Modeling the brain with this level of detail could reveal new insights about the pathogenesis of mental illness.⁴ It would provide a virtual environment in which to conduct experiments, though researchers would need to develop guidelines regarding the ethics of these experiments, since such a construct may possess a form of consciousness. This virtual connectome could also vastly accelerate studies of human intelligence, leading to the possibility of implementing this new understanding of cognition in artificial intelligence and even developing intelligent machines. Brain-computer interfaces (BCIs) may also benefit from WBE since more precise neuronal codes for coding motor actions and sensory information could be uncovered. By studying WBEs, the “language” of the brain’s operations could be revealed and may give rise to a rich array of new advances. On a scale which parallels the space program and the Human Genome Project, neuroscience may be approaching a revolution.

Foundations of Computational Neuroscience

Biologically accurate neuronal simulations usually employ conductance-based models. The canonical conductance-based model developed by Alan Hodgkin and Andrew Huxley was published in 1952,⁵ and would win them the Nobel Prize in Physiology or Medicine. Current models still use the core principles from the Hodgkin-Huxley model.⁶ This model is a differential equation which takes into account the conductances and equilibrium potentials of neuronal sodium channels, potassium channels, and channels that transport anions across the cell membrane.⁵ Conductance is defined as the inverse of electrical resistance and an equilibrium potential is the electrical potential energy across a membrane at equilibrium. The output of this equation is the total current across the membrane of the neuron, which can be converted to a voltage by multiplying by the total membrane resistance. The Hodgkin-Huxley equation can generate biologically accurate predictions for the membrane voltage of a neuron at a given time. Using these membrane voltages and the firing threshold of the neuron in question, the timing of action potentials can be computationally predicted, allowing neural activity to be simulated.

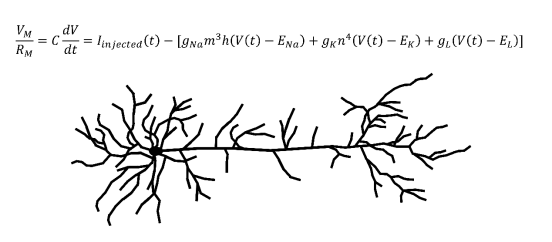
Another important concept in computational neuroscience is the multi-compartmental model. Consider an axon which synapses onto another neuron’s dendrite. When the axon terminal releases neurotransmitters which depolarize (move the membrane potential closer to zero) the other neuron’s dendritic membrane, the depolarization will need to travel down the dendrite, past the soma, and onto the axon of this post-synaptic neuron to contribute to the initiation of an action potential. Since the density of voltage-gated channels outside of the axon is relatively low, the depolarization decreases as it moves along this path. In order to accurately recreate a biological neuron in a computer, this process must also be modeled. To accomplish this, the model segments each portion of the neuronal membrane into multiple “compartments.” In general, increasing the number of compartments improves the accuracy of the model, but requires more computational power. Multi-compartmental models use more complicated partial differential equation extensions of the Hodkin-Huxley equation. When solved, the resulting multivariable functions uses both the location along the dendrite and the time to predict depolarization behavior, which is inputted to the postsynaptic virtual neuron.

These methods form the fundamentals for constructing simulated neurons and assemblies of neurons. They have shown remarkable biological fidelity even in complex simulations. Multi-compartmental Hodgkin-Huxley models, given the proper parameters from experimental data, can make predictive approximations of biological activity.

The Blue Brain Project

The quest to simulate the human brain has largely emerged from The Blue Brain Project, a collaboration headed by Henry Markram. In 2007, Markram announced the completion of the Blue Brain Project’s first phase, the detailed simulation of a rat neocortical column in IBM’s Blue Gene supercomputer. This achievement required a powerful engineering strategy that integrated the many components of the simulation.⁶ To start, gene expression data were used to determine ion channel distributions in the membranes of various types of cortical neuron. Over twenty different types of ion channel were considered in this analysis. These ion channels were incorporated into extensions of the Hodgkin-Huxley model. Three-dimensional neuron morphologies were paired with appropriate ion channel distributions and a database of virtual neuron subtypes was assembled. Experimental data on axon and dendrite locations was collected to recreate the synaptic connections in the neocortical column. A collision detection algorithm was employed to adjust the three-dimensional arrangement of axons and dendrites by “jittering” them until they matched the experimental data. This allowed the column’s structure to be reconstructed. Physiological recordings provided membrane conductances, probabilities of synaptic release, and other biophysical parameters necessary to model each neuronal subtype. In addition, plasticity rules mirroring those found in biological neurons were applied to the virtual neurons to allow them to perform learning. Parameters were optimized through a series of iterative tests and corrections.

By 2012, the project reached another milestone,⁷ the simulation of a larger brain structure known as a cortical mesocircuit that consisted of over 31,000 neurons in several hundred “minicolumns.” In this simulation, some of the details of synaptic connectivity were algorithmically predicted based on experimental data rather than strictly adhering to experimentally generated maps. Nevertheless, valuable insights were produced from the emulated mesocortical circuit. In vivo systems have shown puzzling bursts of uncorrelated activity. The simulation confirmed that this emergent property occurred as a consequence of destructive interference between excitatory and inhibitory signals. The simulation also demonstrated that, during moments of imbalance between these signals, choreographed patterns of neuronal encoding can occur within the “overspill.” Such observations in this virtual cortical circuit have increased understanding of the mechanisms of neural activity.

The Human Brain Project

As the Blue Brain Project developed, it was eventually rebranded as The Human Brain Project (HPB) to reflect its overarching goal. In 2013, the HBP was selected as a European Union Flagship project and granted over 1 billion euros in funding (equivalent to slightly more than 1 billion USD). Criticisms inevitably arose. Some scientists feared that it would divert funding from other areas of research.⁸ A major complaint was that the HBP was ignoring experimental neuroscience in favor of simulations. The simulation approach would need to be complemented by further data collection efforts since structural and functional mapping information is lacking. As a result, the HBP restructured to broaden its focus. An array of neuroscience platforms with varying levels of experimental and computational focus were developed.⁹ The Mouse Brain Organization and Human Brain Organization Platforms were initiated to further knowledge of brain structure and function through more experimentally centered approaches. The Systems and Cognitive Neuroscience Platform employed both computational and experimental approaches to study behavioral and cognitive phenomena such as context-dependent object recognition. The Theoretical Neuroscience Platform and Brain was created to build large computational models starting at the cellular level, closely mirroring the original Blue Brain Project.

In addition to these, several overlapping platforms were initiated.⁹ The Neuroinformatics Platform seeks to organize databases containing comprehensive information on rodent and human brains as well as three-dimensional visualization tools. The High Performance Analytics and Computing Platform (HPAC) centers on managing and expanding the supercomputing resources involved in the HBP. In the longer term, HPAC may help the HBP obtain exascale computers, capable of running at least a quintillion floating point operations per second. Exascale computers would have the ability to simulate the entire human brain at the high level of detail found in the first simulated neocortical column from 2007.⁴ The Medical Informatics platform focuses on collecting and analyzing medically relevant brain data, particularly for diagnostics.⁹ The Brain Simulation Platform is related to the Theoretical Neuroscience Platform, but more broadly explores models at differing resolutions (i.e. molecular, subcellular, simplified cellular, and models which switch between resolutions during the simulation). The Neuromorphic Computing Platform tests models using computer hardware that more closely approximates the organization of nervous tissue than traditional computing systems. Finally, the Neurorobotics Platform develops simulated robots which use brain-inspired computational strategies to maneuver in their virtual environments.

Through the introduction of these platforms, the HBP collaborative may yield new insights in diverse areas of neuroscience and neurotechnology. The HBP’s original mission of simulating the human brain will continue, but with along a more interdisciplinary path. The incorporation of experimental emphases may help build more complete maps of the brain at multiple scales, enabling the development of superior simulated models as the project evolves.

The Future

As a European Flagship, the HBP will receive funding over a ten year period that started in 2013.⁹ It may yield advances in numerous neuroscientific fields as well as in computer science and robotics. The HBP is also open to further collaboration with other neuroscience projects such as the American BRAIN Initiative. The Theoretical Neuroscience and Brain Simulation platforms may unify experimental knowledge and pave the way to emulating a brain in a supercomputer. As exascale supercomputers emerge and the human connectome continues to be revealed, this challenging goal may be achievable. With the massive funding and resources available, the HBP may significantly advance understanding of the human brain and its operations.

The eventual completion of the HBP may have tremendous implications for the more distant future. Insights into brain mechanisms may help to decipher the mystery of consciousness. Such understanding may open the door to constructing intelligent machines.⁴ With the capacity to emulate consciousness in a computational substrate, prosthetic neurotechnologies¹⁰ may see remarkable advances. We may uncover methods for gradually replacing portions of the brain with equivalent computational processing systems, enabling mind uploading. Although these possibilities currently seem fantastical, exponential trends in technological advancement¹¹ suggest that they may transition into real possibilities within the next hundred years. The HBP demonstrates that collaborative innovation is vital for building the future and continuing the human quest to invent, experience, and discover.

References

(1) Azevedo, F. A., Carvalho, L. R., Grinberg, L. T., Farfel, J. M., Ferretti, R. E., Leite, R. E., Jacob, W. F., Lent, R., Herculano-Houzel, S. (2009). Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. The Journal of Comparative Neurology, 513(5), 532-541. doi:10.1002/cne.21974

(2) Pakkenberg, B. (2003). Aging and the human neocortex. Experimental Gerontology, 38(1-2), 95-99. doi:10.1016/s0531-5565(02)00151-1

(3) Grillner, S., Ip, N., Koch, C., Koroshetz, W., Okano, H., Polachek, M., Mu-Ming, P., Sejnowski, T. J. (2016). Worldwide initiatives to advance brain research. Nature Neuroscience, 19(9), 1118-1122. doi:10.1038/nn.4371

(4) Markram, H., Meier, K., Lippert, T., Grillner, S., Frackowiak, R., Dehaene, S., Knoll, A., Sompolinsky, H., Verstreken, K., DeFelipe, J., Grant, S., Changeux, J., Saria, A. (2011). Introducing the Human Brain Project. Procedia Computer Science, 7, 39-42. doi:10.1016/j.procs.2011.12.015

(5) Hodgkin, A. L., & Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology, 117(4), 500-544. doi:10.1113/jphysiol.1952.sp004764

(6) Markram, H. (2006). The Blue Brain Project. Nature Reviews Neuroscience, 7(2), 153-160. doi:10.1038/nrn1848

(7) Markram, H., Muller, E., Ramaswamy, S., Reimann, M., Abdellah, M., Sanchez, C., … Schürmann, F. (2015). Reconstruction and Simulation of Neocortical Microcircuitry. Cell, 163(2), 456-492. doi:10.1016/j.cell.2015.09.029

(8) Frégnac, Y., & Laurent, G. (2014). Neuroscience: Where is the brain in the Human Brain Project? Nature, 513(7516), 27-29. doi:10.1038/513027a

(9) Amunts, K., Ebell, C., Muller, J., Telefont, M., Knoll, A., & Lippert, T. (2016). The Human Brain Project: Creating a European Research Infrastructure to Decode the Human Brain. Neuron, 92(3), 574-581. doi:10.1016/j.neuron.2016.10.046

(10) Deadwyler, S. A., Hampson, R. E., Song, D., Opris, I., Gerhardt, G. A., Marmarelis, V. Z., & Berger, T. W. (2016). A cognitive prosthesis for memory facilitation by closed-loop functional ensemble stimulation of hippocampal neurons in primate brain. Experimental Neurology. doi:10.1016/j.expneurol.2016.05.031

(11) Kurzweil, R. (2005). The Singularity is Near: When Humans Transcend Biology. New York: Viking.

(12) Chalmers, D. J. (2014). Uploading: A Philosophical Analysis. Intelligence Unbound, 102-118. doi:10.1002/9781118736302.ch6

(13) [The IBM Blue Gene/P supercomputer installation at the Argonne Leadership Angela Yang Computing Facility located in the Argonne National Laboratory, in Lemont, Illinois, USA.]. (2007, December 10). Retrieved June 20, 2017, from wikimedia.org